See https://docs.google.com/presentation/d/1E0i1tI0gzUbxS1BNxaoCdVlu5ZpZ8A_D/edit#slide=id.p1
Category: teaching
SUMMARY
The speaker discusses how maladaptive perfectionism hinders time management for PhD students and provides strategies to overcome it.
IDEAS:
- Perfectionism builds self-esteem but can hinder productivity and time management for PhD students.
- Maladaptive perfectionism creates unnecessary rules that restrict daily productivity and progress.
- Responding immediately to emails can waste time; it’s better to batch email responses.
- Prioritizing one or two significant tasks daily can reduce overwhelm and improve focus.
- Energy levels fluctuate throughout the day, affecting when to tackle challenging tasks.
- Saying no to non-prioritized tasks can free up time for essential responsibilities.
- Batching similar tasks enhances focus and minimizes distractions from constant notifications.
- Perfectionism leads to either paralysis or burnout, both detrimental to academic progress.
- Many PhD-related tasks contribute to busyness rather than actual productivity.
- Academic CVs benefit more from published papers than organizing symposia or events.
- Understanding when to focus on high-energy tasks is crucial for effective time management.
- Collaborating selectively on papers can prevent wasted time and effort.
- Automation tools can assist with repetitive tasks, improving overall efficiency.
- Prioritizing two anchor tasks allows flexibility to manage smaller tasks throughout the day.
- Procrastination can sometimes reveal the true importance of tasks that demand attention.
- Multitasking leads to distraction; focusing on one task at a time enhances productivity.
INSIGHTS:
- Maladaptive perfectionism can create rules that stifle productivity and complicate time management.
- Prioritizing tasks based on energy levels optimizes performance and mitigates burnout risks.
- Batching tasks helps maintain focus and prevents the distraction of constant interruptions.
- Saying no strategically can protect time for significant academic responsibilities.
- Collaboration should be selective to ensure contributions lead to tangible outcomes.
- Understanding the nature of perceived urgency can help manage time effectively.
- Focusing on meaningful tasks rather than busywork is essential for PhD success.
- Recognizing the impact of perfectionism on decision-making can alleviate procrastination.
- Setting boundaries with supervisors is necessary for maintaining academic priorities.
- Building self-awareness around personal energy levels can enhance task management.
QUOTES:
- “Maladaptive perfectionism causes you to create loads of rules for yourselves.”
- “Perfectionism tends to lead to either complete paralysis or burnout.”
- “We love saying ohoh I’m so busy because Society has told us if you’re busy you’re important.”
- “You need to work out when you have the most energy and work with your own daily energy flux.”
- “Saying no more often means that you’re going to free up time to focus on what you should be doing.”
- “A lot of times you can say no I don’t have time for that that is not my priority.”
- “Sometimes the loud things in your mind aren’t the important things.”
- “Batching means that you can focus on one task and if someone really wants to get hold of you, they’ll be able to find you.”
- “Turn off your notifications, don’t look at emails and look at them maybe mid-morning and after lunch.”
- “Multitasking is a massive pain in the bum bum.”
- “You’ll find your time management skills and your productivity will go through the roof.”
- “If you only have to do three of them or even two of them, which two would you choose?”
- “Understanding who is actually true to their word is essential in academic collaborations.”
- “Perfectionism creates narratives about what will happen if we don’t follow these rules.”
- “It’s very rare that an urgent email comes in where you need to respond to this in the next 5 seconds.”
HABITS:
- Prioritize one significant task in the morning and another in the afternoon daily.
- Use energy levels to determine the timing of focused, demanding tasks.
- Batch similar tasks together to minimize distractions and improve efficiency.
- Respond to emails at designated times rather than immediately to enhance focus.
- Say no to non-prioritized requests to protect valuable time for essential tasks.
- Turn off notifications to reduce interruptions during important work sessions.
- Write down and prioritize tasks to manage workload and reduce overwhelm.
- Automate repetitive tasks using available AI tools to enhance productivity.
- Test the limits of personal rules and challenge perfectionist tendencies regularly.
- Create a structured schedule that accommodates varying energy levels throughout the day.
- Collaborate selectively on projects to ensure productive outcomes without wasted effort.
- Establish clear boundaries with supervisors regarding task management and priorities.
- Focus on completing significant tasks before engaging in smaller, low-energy activities.
- Acknowledge and challenge perfectionist thoughts that lead to procrastination or stress.
- Set specific times for reading and writing to ensure dedicated focus on these tasks.
- Reflect on daily accomplishments to build self-esteem without falling into perfectionism traps.
FACTS:
- Many PhD tasks contribute to busywork rather than real academic progress.
- Perfectionism can lead to significant burnout or paralysis in decision-making.
- Academic success is more significantly impacted by published papers than organizing events.
- Time management issues often stem from societal pressures to appear busy and important.
- Batching tasks can improve overall productivity and reduce mental fatigue.
- Energy levels throughout the day influence the effectiveness of task completion.
- Responding to emails immediately often leads to unnecessary distractions and lost focus.
- Collaboration is vital, but not all requests lead to fruitful academic outcomes.
- Saying no is necessary to prioritize tasks that genuinely advance academic careers.
- Perfectionism often creates unrealistic expectations that can hinder performance and well-being.
- Automation tools can significantly enhance efficiency in managing academic workloads.
- Daily productivity can improve by focusing on only one or two significant tasks.
- Multitasking is generally counterproductive and should be avoided for better focus.
- Maintaining a structured schedule can alleviate the chaos of academic life.
- Understanding personal working styles can help optimize time management strategies.
- Prioritizing meaningful tasks helps cultivate a more fulfilling academic experience.
REFERENCES:
- The Five Habits for Monster PhD productivity video mentioned by the speaker.
- AI tools for academics discussed in the context of automation and efficiency.
- Various techniques for managing time and tasks effectively in academia.
ONE-SENTENCE TAKEAWAY
Maladaptive perfectionism significantly impairs time management for PhD students, but strategic prioritization can enhance productivity.
RECOMMENDATIONS:
- Challenge perfectionist tendencies by sending emails without excessive revisions or delays.
- Schedule high-energy tasks for when personal energy levels are at their peak.
- Prioritize significant daily tasks and let less important ones fade into the background.
- Use batching for emails and tasks to maintain focus and prevent distraction.
- Practice saying no to non-essential requests to protect academic priorities and time.
- Automate repetitive tasks using AI tools to streamline workflow and enhance efficiency.
- Reflect on daily achievements to build confidence without succumbing to perfectionism.
- Create a structured routine that accommodates personal energy fluctuations throughout the day.
- Collaborate selectively to ensure efforts yield meaningful academic contributions.
- Turn off notifications during focused work sessions to minimize interruptions and distractions.
- Be selective about which additional responsibilities to accept based on career goals.
- Test personal limits regarding task completion to overcome perfectionist fears.
- Set aside dedicated time for reading and writing to ensure consistent progress.
- Recognize the difference between urgent and important tasks to manage priorities effectively.
- Embrace the idea that perceived failures often have minimal impact on overall performance.
- Foster an understanding that busywork does not equate to productivity in academic settings.
This is a rather good read for anyone interested in reproducible research (i.e., everyone who tries to become a researcher as a career)
TLDR:
Why reproducible research
- reproducible research helps researchers remember how and why they performed specific analyses during the course of a project.
- reproducible research enables researchers to quickly and simply modify analyses and figures.
- reproducible research enables quick reconfiguration of previously conducted research.
- conducting reproducible research is a strong indicator to fellow researchers of rigor, trustworthiness, and transparency in scientific research.
- reproducible research increases paper citation rates (Piwowar et al. 2007, McKiernan et al. 2016) and allows other researchers to cite code and data in addition to publications.
A three-step framework for conducting reproducible research
Before data analysis: data storage and organization
- data should be backed up at every stage of the research process and stored in multiple locations.
- Digital data files should be stored in useful, flexible, portable, nonproprietary formats.
- It is often useful to transform data into a “tidy” format (Wickham 2014) when cleaning up and standardizing raw data.
- Metadata explaining what was done to clean up the data and what each of the variables means should be stored along with the data.
- Finally, researchers should organize files in a sensible, user-friendly structure and make sure that all files have informative names.
- Throughout the research process, from data acquisition to publication, version control can be used to record a project’s history and provide a log of changes that have occurred over the life of a project or research group.
During analysis: best coding practices
- When possible, all data wrangling and analysis should be performed using coding scripts—as opposed to using interactive or point-and-click tools—so that every step is documented and repeatable by yourself and others.
- Analytical code should be thoroughly annotated with comments.
- Following a clean, consistent coding style makes code easier to read.
- There are several ways to prevent coding mistakes and make code easier to use.
- First, researchers should automate repetitive tasks.
- Similarly, researchers can use loops to make code more efficient by performing the same task on multiple values or objects in series
- A third way to reduce mistakes is to reduce the number of hard-coded values that must be changed to replicate analyses on an updated or new data set.
- create a software container, such as a Docker (Merkel 2014) or Singularity (Kurtzer et al. 2017) image (Table 1) for ensuring that analyses can be used in the future
After data analysis: finalizing results and sharing
- produce tables and figures directly from code than to manipulate these using Adobe Illustrator, Microsoft PowerPoint, or other image editing programs. (comment: for example, can use csvsimple package in latex)
- make data wrangling, analysis, and creation of figures, tables, and manuscripts a “one-button” process using GNU Make (https://www.gnu.org/software/make/).
- To increase access to publications, authors can post preprints of final (but preacceptance) versions of manuscripts on a preprint server, or postprints of manuscripts on postprint servers.
- Data archiving in online general purpose repositories such as Dryad, Zenodo, and Figshare
Useful Links
Below is a message from Ali Rhoades, an experiential learning coordinator.
For students interested in career readiness and job searches, I would encourage them to look into our events page including our Careerapalooza, Career Fair, and other events. Our Careerapalooza is coming up (next Thursday) but this would be a great opportunity for students to informally meet our staff, learn more about our support services (including applying for internship) and join a career community.
Our office just recently launched our Career Communities model, which encourages students to lean into finding internships and jobs specific to their passions and industry, instead of stressing to find experiential learning opportunities strict to their major. For example, if an engineering student was passionate for working in nonprofit, they would find tailored opportunities through their Nonprofit Career Community. This link will also provide them with access to their Handshake accounts (all OU students have free access to this internship and job board) including other helpful resources such as an advisor, additional job posting websites, and career readiness tips. Handshake will be the source where OU posts jobs, internships, externships, co-ops, and fellowships, which has new postings daily. If you would like one of our staff members to visit with your class to share more information about Career Communities and Handshake, please let me know-I’d be happy to set that up for you.
As for micro-internships: OU Career Center will be partnering with Parker Dewey soon, hopefully by the end of September, to have tailored micro-internships exclusively to OU students for local, remote, and regional opportunities that are short term and project based. Until then, students can look for public opportunities through Parker Dewey’s website here.
Define policy ![]() and transition probability
and transition probability ![]() , the probability of a trajectory
, the probability of a trajectory ![]() equal to
equal to
![Rendered by QuickLaTeX.com \[\pi_\theta(\tau) = \rho_0(s_0)\prod_{t=0}^{T-1}P(s_{t+1}|s_t,a_t)\pi_\theta(a_t|s_t)\]](https://outliip.org/wp-content/ql-cache/quicklatex.com-e5c1955a676700c318177440c58af10b_l3.png)
Denote the expected return as ![]() . Let’s try to find the improve a policy through gradient ascent by updating
. Let’s try to find the improve a policy through gradient ascent by updating
![]()
Policy gradient and REINFORCE
Let’s compute the policy gradient ![]() ,
,
(1) ![Rendered by QuickLaTeX.com \begin{align*} \nabla_\theta J(\theta)& =\nabla_\theta E_{\tau \sim \pi_\theta}[r(\tau)] = \nabla_\theta \int \pi_\theta(\tau) r(\tau) d\tau \\ &=\int \nabla_\theta \pi_\theta(\tau) r(\tau) d\tau =\int \pi_\theta(\tau) \nabla_\theta \log \pi_\theta(\tau) r(\tau) d\tau \\ &=E_{\tau \sim \pi_\theta}\left[ \nabla_\theta \log \pi_\theta(\tau) r(\tau) \right] \\ &=E_{\tau \sim \pi_\theta}\left[ \nabla_\theta \left[\rho_0(s_0) + \sum_t \log P(s_{t+1}|s_t,a_t) \right. \right. \\ & \qquad \left. \left. +\sum_{t}\log \pi_\theta(a_t|s_t)\right] r(\tau) \right]\\ &=E_{\tau \sim \pi_\theta}\left[ \left(\sum_{t} \nabla_\theta \log \pi_\theta(a_t|s_t)\right) r(\tau) \right]\\ &=E_{\tau \sim \pi_\theta}\left[ \left(\sum_{t}\nabla_\theta \log \pi_\theta(a_t|s_t)\right) \left(\sum_t \gamma^t r(s_t,a_t)\right) \right] \end{align*}](https://outliip.org/wp-content/ql-cache/quicklatex.com-f8ed79144d20ea2c0b08fea13eb1d9bc_l3.png)
With ![]() trajectories, we can approximate the gradient as
trajectories, we can approximate the gradient as
![Rendered by QuickLaTeX.com \[\nabla_\theta J(\theta) \approx \frac{1}{N} \sum_{i=1}^N \left( \sum_t \nabla_\theta \log \pi_\theta(a_t|s_t)\right) \left( \sum_t \gamma^t r(s_t,a_t)\right)\]](https://outliip.org/wp-content/ql-cache/quicklatex.com-ba7359d9faa0753ea024fa40f4361ee2_l3.png)
The resulting algorithm is known as REINFORCE.
Actor-critic algorithm
One great thing about the policy-gradient method is that there is much less restriction on the action space than methods like Q-learning. However, one can only learn after a trajectory is finished. Note that because of causality, reward before the current action should not be affected by the choice of policy. So we can write the policy gradient approximate in REINFORCE instead as
(2) ![Rendered by QuickLaTeX.com \begin{align*} \nabla_\theta J(\theta) &= E_{\tau \sim \pi_\theta}\left[ \left(\sum_{t=0}^T\nabla_\theta \log \pi_\theta(a_t|s_t)\right) \left(\sum_{t'=0}^T \gamma^{t'} r(s_{t'},a_{t'})\right) \right] \\ &\approx E_{\tau \sim \pi_\theta}\left[ \sum_{t=0}^T\nabla_\theta \log \pi_\theta(a_t|s_t)\sum_{t'=t}^T \gamma^{t'} r(s_{t'},a_{t'})\right]\\ &\approx E_{\tau \sim \pi_\theta}\left[ \sum_{t=0}^T\nabla_\theta \log \pi_\theta(a_t|s_t) \gamma^t \sum_{t'=t}^T \gamma^{(t'-t)} r(s_{t'},a_{t'})\right] \\ &\approx E_{\tau \sim \pi_\theta}\left[ \sum_{t=0}^T\nabla_\theta \log \pi_\theta(a_t|s_t) \gamma^t Q(a_t,s_t)\right] \end{align*}](https://outliip.org/wp-content/ql-cache/quicklatex.com-1b5a5a7e2575d2f99d0a3faecd5a5bcc_l3.png)
Rather than getting the reward from the trajectory directly, an actor-critic algorithm can estimate the return with a critic network ![]() . So the policy gradient could be instead approximated by (ignoring discount
. So the policy gradient could be instead approximated by (ignoring discount ![]() )
)
![Rendered by QuickLaTeX.com \[\nabla_\theta J(\theta) \approx E\left[\sum_{t=0}^T \nabla_\theta \log \underset{\mbox{\tiny actor}}{\underbrace{\pi_\theta(a_t|s_t)}} \underset{\mbox{\tiny critic}}{\underbrace{Q(a_t,s_t)}}\right]\]](https://outliip.org/wp-content/ql-cache/quicklatex.com-04837471244ff8ed13908b1a48b1ba7f_l3.png)
Advantage Actor Critic (A2C)
One problem of REINFORCE and the original actor-critic algorithm is high variance. To reduce the variance, we can simply subtract ![]() by its average over the action
by its average over the action ![]() . The difference
. The difference ![]() is known as the advantage function and the resulting is known as the Advantage Actor Critic algorithm. That is the policy gradient will be computed as
is known as the advantage function and the resulting is known as the Advantage Actor Critic algorithm. That is the policy gradient will be computed as
![Rendered by QuickLaTeX.com \[\nabla_\theta J(\theta) \approx E\left[ \sum_{t=0}^T \nabla_\theta \log \pi_\theta(a_t|s_t) A(s_t,a_t)\right]\]](https://outliip.org/wp-content/ql-cache/quicklatex.com-1058a3778206fa4ebefb9e337213664b_l3.png)
instead.
Reference:
Dong has given a very nice talk (slides here) on reinforcement learning (RL) earlier. I learned Q-learning from an online Berkeley lecture several years ago. But I never had a chance to look into SARSA and grasp the concept of on-policy learning before. I think the talk sorted out some of my thoughts.
A background of RL
A typical RL problem involves the interaction between an agent and an environment. The agent will decide on an action based on the current state as it interacts with the environment. Based on this action, the model reaches a new state stochastically with some reward. The agent’s goal is to devise a policy (i.e., determining what action to take under each state) that maximizes the total expected reward. We usually model this setup as the Markov decision process (MDP), where the probability of reaching the next state ![]() only depends on the current state
only depends on the current state ![]() and current choice of action
and current choice of action ![]() (independent of all earlier states) and hence is a Markov model.
(independent of all earlier states) and hence is a Markov model.
Policy and value functions
A policy ![]() is just a mapping from each state
is just a mapping from each state ![]() to an action
to an action ![]() . The value function is defined as the expected utility (total reward) of a state given a policy. There are two most common value functions: the state-value function,
. The value function is defined as the expected utility (total reward) of a state given a policy. There are two most common value functions: the state-value function, ![]() , which is the expected utility given the current state and policy, and the action-value function,
, which is the expected utility given the current state and policy, and the action-value function, ![]() , which is the expected utility given the current action, current state, and policy.
, which is the expected utility given the current action, current state, and policy.
Q-Learning
The main difference of RL from MDP is that the probability ![]() is not known in general. If we know this and also the reward
is not known in general. If we know this and also the reward ![]() for each state, current action, and next state, we can compute the expected utility for any state and appropriate action always. For Q-learning, the goal is precisely to estimate the Q function for the optimal policy by updating Q as
for each state, current action, and next state, we can compute the expected utility for any state and appropriate action always. For Q-learning, the goal is precisely to estimate the Q function for the optimal policy by updating Q as
![]()
where we have ![]() to control the degree of exponential smoothing in approximating
to control the degree of exponential smoothing in approximating ![]() . When
. When ![]() , we do not use exponential smoothing at all.
, we do not use exponential smoothing at all.
Note that the equation above only describes how we are going to update ![]() , but it does not describe what action should be taken. Of course, we can exploit the estimate of
, but it does not describe what action should be taken. Of course, we can exploit the estimate of ![]() and select the action that maximizes it. However, the early estimates of
and select the action that maximizes it. However, the early estimates of ![]() is bad and so exploiting will work very poorly. Instead, we may simply select the action
is bad and so exploiting will work very poorly. Instead, we may simply select the action ![]() randomly initially. And as the prediction of
randomly initially. And as the prediction of ![]() improves, exploit the knowledge of
improves, exploit the knowledge of ![]() and take the action maximizing
and take the action maximizing ![]() at times. This is the exploration vs exploitating trade-off. We often denote the probability of exploitation as
at times. This is the exploration vs exploitating trade-off. We often denote the probability of exploitation as ![]() and we set an algorithm is
and we set an algorithm is ![]() -greedy when with a probability of
-greedy when with a probability of ![]() that the best action according to the current estimate of
that the best action according to the current estimate of ![]() is taken.
is taken.
On policy/Off-policy
In Q-learning, the Q-value is not updated according to data obtained from the actual action that has been taken. There are two terminologies that sometimes confuse me.
- Behavior policy: policy that actually determines the next action
- Target policy: policy that used to evaluate an action and that we are trying to learn
For Q-learning, the behavior policy and target policy apparently are not the same as the action that maximizes ![]() does not necessarily be the action that was actually taken.
does not necessarily be the action that was actually taken.
SARSA
Given an experience ![]() (that is why it is called SARSA), we update an estimate of Q instead by
(that is why it is called SARSA), we update an estimate of Q instead by
![]()
It is on-policy as the data used to update ![]() (target policy) is directly from the behavior policy that was used to generate the data
(target policy) is directly from the behavior policy that was used to generate the data
Off-policy has the advantage to be more flexible and sample efficient but it could be less stable as well (see [6], for example).
Reference:
-
[1] Off Policy vs On Policy Agent Learner – Reinforcement Learning – Machine Learning
-
[2] Off-policy vs On-Policy vs Offline Reinforcement Learning Demystified!
- [4] Off-policy learning
-
[5] The False Promise of Off-Policy Reinforcement Learning Algorithms
- [6] Off-policy versus on-policy RL
Here I will derive Kalman filter from belief propagation (BP). While I won’t derive exactly the closed-form expression as Kalman filter, one can verify numerically that the BP procedure below is the same as the standard Kalman filter. For derivation to the exact same expression, please see here.
Kalman filter is a special case of Gaussian BP. It can be easily understood as three different propagation steps as below.
Scenario 1: Passing message from 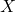 to
to 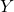 for
for 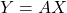
Say ![]() ,
, ![]() . And as
. And as
![]()
![]() .
.
Therefore, ![]() .
.
Scenario 2: Passing message from 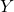 back to
back to 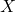 for
for 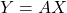
This is a bit trickier but still quite simple. Let the covariance of ![]() be
be ![]() . And from the perspective of
. And from the perspective of ![]() ,
,
![]()
![]()
![]()
![]()
![]()
Thus, ![]()
Scenario 3: Combining two independent Gaussian messages
Say one message votes for ![]() and precision
and precision ![]() (precision is the inverse of the covariance matrix). And say another message votes for
(precision is the inverse of the covariance matrix). And say another message votes for ![]() and precision
and precision ![]() .
.
Since
![]()
![]()
![]()
![]()
Thus, ![]()
BP for Kalman update
Let’s utilize the above to derive the Kalman update rules. We will use almost exactly the same notation as the wiki here. We only replace ![]() by
by ![]() and
and ![]() by
by ![]() to reduce cluttering slightly.
to reduce cluttering slightly.
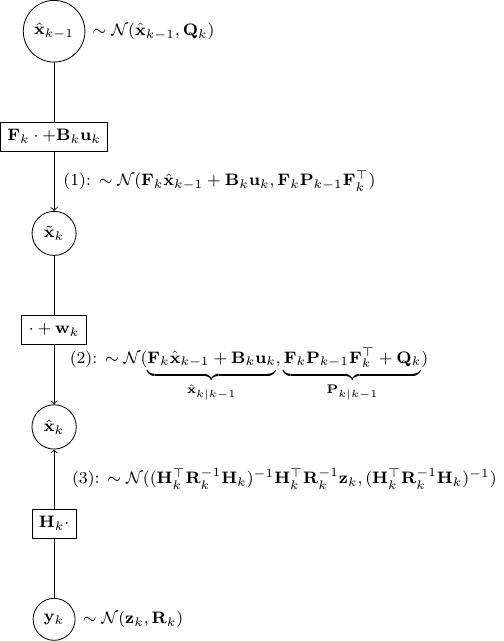
- As shown in the figure above, given
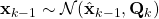 and
and 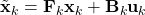 , we have as in (1)
, we have as in (1)
![Rendered by QuickLaTeX.com \[\tilde{\bf x}_k \sim \mathcal{N}({\bf F}_k \hat{\bf x}_{k-1} + {\bf B}_k {\bf u}_k, {\bf F}_k {\bf P}_{k-1}{\bf F}_k^\top)\]](https://outliip.org/wp-content/ql-cache/quicklatex.com-53c4647000975eab4573bbd27baa466c_l3.png)
as it is almost identical to Scenario 1 besides a trivial constant shift of
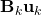 .
. - Then step (2) is obvious as,
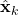 is nothing but
is nothing but 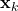 added by a noise of covariance
added by a noise of covariance 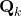 .
. - Now, step (3) is just a direct application of Scenario 2.
Finally, we should combine the estimate from (2) and (3) as independent information using the result in Scenario 3. This gives us the final a posterior estimate of ![]() as
as
![Rendered by QuickLaTeX.com \[\mathcal{N}\left(\Sigma({\bf P}_{k|k-1}^{-1} \hat{\bf x}_{k|k-1} +{\bf H}_k^\top {\bf R}_k^{-1} {\bf z}_k),\underset{\Sigma}{\underbrace{({\bf P}^{-1}_{k|k-1}+{\bf H}^\top_k {\bf R}^{-1}_k {\bf H}_k)^{-1}}}\right)\]](https://outliip.org/wp-content/ql-cache/quicklatex.com-f728e11ea7c6193a812c8c9305dcdd48_l3.png)
Although it is not easy to show immediately, one can verify numerically that the ![]() and the mean above are indeed
and the mean above are indeed ![]() and
and ![]() in the original formulation, respectively.
in the original formulation, respectively.
Came across two different network architectures that I think can discuss together as I feel that they share a similar core idea. Extract and leverage some global information from the data with global pooling.
PointNet
The objective of PointNet is to classify each voxel of a point cloud and detect the potential object described by the point cloud. Consequently, each voxel can belong to a different semantic class but they all share the same object class.
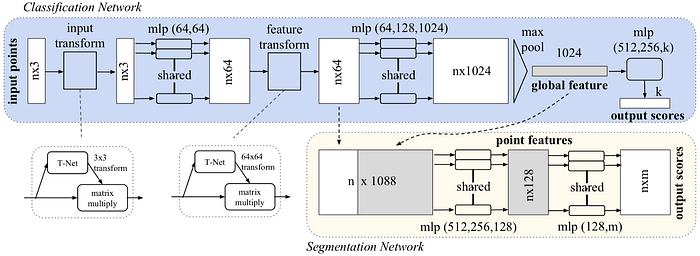
One important property of the point cloud is that all points are not in any particular order. Therefore, it does not make too much sense to train a convolutional layer or fully connected layer to intermix the point. The simplest reasonable operation to combine all information is just pooling (max or average). For PointNet, each point is first individually processed and then a global feature is generated using max pooling. The object described by the point cloud is also classified by the global feature.
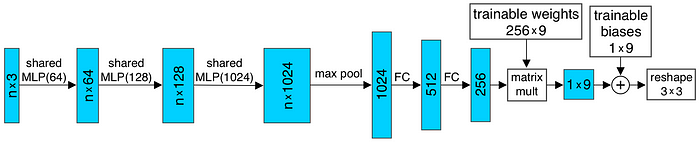
And the input transform and feature transform in the above figure are trainable and will be adapted to the input. This serves the purpose of aligning the point cloud before classification. For example, the T-Net in the input transform is elaborated as shown below.
To classify individual voxel, the global feature is combined with the local feature also generated earlier in the classification network. The combined feature of each voxel will be individually processed into point features, which are then used to classify the semantic class of the voxel.
SENet
SENet was the winner of the classification competition of ImageNet competition in 2017. It reduces the top-5 error rate to 2.251% from the prior 2.991%. The key contribution of SENet is the introduction of the SENet module as follows

The basic idea is very simple. For a feature tensor with $latex C$ channel, we want to adaptively adjust the contribution from each channel through training. Since there is no restriction in the order of the data inside the channel, the most rational thing to summarize that information is simply through pooling. For SE Net module, it is simply done with an average pooling (squeezing). The “squeezed” data are then used to estimate the contribution of each channel (different levels of “excitation”). The computed weights are then used to scale the values of each channel. This SE module can be applied in literally everywhere. For example, it can be combined with inception module to form SE-inception module or ResNet module to form SE-ResNet module as shown below.


Motivation
While Monte Carlo methods have lots of potential applications, we will just name two here as a motivation:
- Data generation. The generated data can be used for simulation or for visualization purposes.
- Inference. Infer unknown variables from observations.
For the first application, the use of Monte Carlo is rather straight forward. We will assume the model parameters are known and we can sample parameters sequentially with Gibbs sampling as described below. If all conditional distributions can be sampled directly (more explanation below), we can use regular Monte Carlo without the need for MCMC.
For the second application, there is an additional layer of complication as we typically would like to sample from the posterior distribution for efficiency. But often only the likelihood distributions are specified. In that case, we will need to sample from a proposal distribution and MCMC is needed.
Basic Idea of Monte Carlo Methods
Ultimately, almost all Monte Carlo Methods are doing nothing but estimating the expectation of some function ![]() with
with ![]() by
by
![]() ,
,
where the above is guaranteed by the law of large number for sufficiently large ![]() .
.
For example, in the coin-flipping examples in Q1 of HW5, we can estimate the ultimate probability of head by conducting the Monte Carlo experiment and counting the number of head. More precisely, denote ![]() as an indicator function where
as an indicator function where ![]() is 1 when
is 1 when ![]() is head. Then
is head. Then
![]() .
.
The key question here is how we are going to collect samples of ![]() ,
, ![]() . In this coin-flipping setup, the Monte-Carlo simulation is trivial. We can conduct the experiment exactly as in a real setup. That is, first draw a coin from the jar; that corresponds to sample a binary random variable
. In this coin-flipping setup, the Monte-Carlo simulation is trivial. We can conduct the experiment exactly as in a real setup. That is, first draw a coin from the jar; that corresponds to sample a binary random variable ![]() with the specified probability of getting coins
with the specified probability of getting coins ![]() or
or ![]() . Then, based on the outcome of
. Then, based on the outcome of ![]() (i.e., which coin that actually picked), we will draw another binary random variable
(i.e., which coin that actually picked), we will draw another binary random variable ![]() for each coin flip according to the probability of head of the chosen coin.
for each coin flip according to the probability of head of the chosen coin.
In the coin-flipping problem, since we are just drawing binary random variables, we can sample the distribution directly without any issue. But for many continuous distributions except a few special cases, direct sampling them is not possible and more involved sampling techniques are needed as described in the following.
This sequential sampling conditioned on previously specified random variables is generally known as Gibbs sampling. Strictly speaking, it is a form of MCMC as we will show later on. But I think it is more appropriate NOT to consider this simple case as MCMC because there is no convergence issue here as you will see that is generally not the case for MCMC.
Basic Sampling Methods
The key question left is how we can sample data from a distribution. For some standard distributions like Gaussian distribution, we can draw samples directly with some well-developed packages. However, there is no direct way of drawing samples for many regular distributions, not to mention those that do not even have a standard form. There are ways to sample any arbitrary distributions, we will mention a couple of simple ones here.
Rejection Sampling
Probably the simplest sampling method is the rejection sampling. Consider drawing sample ![]() . Select any “sampleable” distribution
. Select any “sampleable” distribution ![]() such that
such that ![]() with some constant
with some constant ![]() . Now, instead of drawing sample from
. Now, instead of drawing sample from ![]() , we will draw from
, we will draw from ![]() instead. However, in order to have the sample appear to have the same distribution of
instead. However, in order to have the sample appear to have the same distribution of ![]() , we will only keep a fraction
, we will only keep a fraction ![]() of
of ![]() whenever
whenever ![]() is drawn and discard the rest. To do this, we simply sample a
is drawn and discard the rest. To do this, we simply sample a ![]() from
from ![]() uniformly after each
uniformly after each ![]() sampled. And keep the current
sampled. And keep the current ![]() only if
only if ![]() .
.
Note that in Q4 of HW5, we are essentially doing some form of rejection sampling. Draw the samples from the prior and the likelihood distributions, and then only accept samples that fit the observations. Rejection sampling is simple but it can be quite inefficient. For example, if the current estimates of variables used in sampling are far from the actual values, the sampled outcome most likely will not match well with the observations and we have to reject lots of samples. That’s why other sampling techniques are needed.
Importance Sampling
Rejection sampling is generally very inefficient as a large number of samples can be discarded. If we only care about computing the expection of some function, then we may not need to discard any sample but adjust the weight of each sample instead. Note that
![Rendered by QuickLaTeX.com E_{X\sim p(x)}[f(X)]=\int f(x) p(x) dx = \int \left[f(x)\frac{p(x)}{q(x)}\right] q(x) dx= E_{X\sim q(x)}\left[f(X)\frac{p(X)}{q(X)}\right]](https://outliip.org/wp-content/ql-cache/quicklatex.com-d44ddc9ce7e912f6d9872ce5cced50c1_l3.png) .
.
Thus, we can estimate the expectation by drawing samples from ![]() and compute weighted average of
and compute weighted average of ![]() instead. And the corresponding weights are
instead. And the corresponding weights are ![]() .
.
Even though we can now utilize all samples, importance sampling has two concerns.
- Unlike rejection sampling, we do not directly draw samples with the desired distribution. So we can use those samples to do other things rather than computing expectations.
- The variance of the estimate can be highly sensitive with the choice of
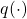 . In particular, since the variance of the estimate is
. In particular, since the variance of the estimate is ![Rendered by QuickLaTeX.com \frac{1}{N}E\left[ f(X)\frac{p(X)}{q(X)}\right]](https://outliip.org/wp-content/ql-cache/quicklatex.com-8dbe52483531c01ca6f87a0182b0ba52_l3.png) , the variance will be especially large if a more probable region in
, the variance will be especially large if a more probable region in 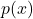 is not covered well by
is not covered well by 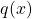 , i.e., we have extensive region where
, i.e., we have extensive region where 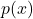 large but
large but 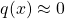 .
.
Markov Chain Monte Carlo
Instead of sampling from ![]() directly, Markov chain Monte Carlo (MCMC) methods try to sample from a Markov chain (essentially a probabilistic state model). Probably the two most important properties of the Markov chain are irreducible and aperiodic. We say a Markov chain is irreducible if we can reach any single state to any other state. And we say a Markov chain is periodic if there exist two states such that one state can reach the other state only in a multiple of
directly, Markov chain Monte Carlo (MCMC) methods try to sample from a Markov chain (essentially a probabilistic state model). Probably the two most important properties of the Markov chain are irreducible and aperiodic. We say a Markov chain is irreducible if we can reach any single state to any other state. And we say a Markov chain is periodic if there exist two states such that one state can reach the other state only in a multiple of ![]() steps with
steps with ![]() . If a Markov chain is not periodic, we say it is aperiodic. Under the above two conditions (aperiodic and irreducible), regardless of the initial state, the distribution of states will converge to the steady-state probability distribution asymptotically as time goes to infinity.
. If a Markov chain is not periodic, we say it is aperiodic. Under the above two conditions (aperiodic and irreducible), regardless of the initial state, the distribution of states will converge to the steady-state probability distribution asymptotically as time goes to infinity.
Consider any two connected states with transition probabilities ![]() (from
(from ![]() to
to ![]() ) and
) and ![]() (from
(from ![]() to
to ![]() ). We say the detailed balance equations are satisfied if
). We say the detailed balance equations are satisfied if ![]() . Note that if detailed balance are satisfied among all states,
. Note that if detailed balance are satisfied among all states, ![]() has to be the steady state probability of state
has to be the steady state probability of state ![]() . Because the probability “flux” going out from
. Because the probability “flux” going out from ![]() to
to ![]() is exactly canceled by the “flux” coming in from
is exactly canceled by the “flux” coming in from ![]() to
to ![]() when the chain reaches this equalibrium.
when the chain reaches this equalibrium.
With the discussion above, we see that one can sample ![]() if we can create a Markov chain with
if we can create a Markov chain with ![]() designed to be the steady-state probability of the chain (by making sure that detailed balance is satisfied). Note that, however, we have to let the chain to run for a while before the probability distribution converges to the steady-state probability. Thus, samples before the chain reaching equilibrium are discarded. This initial step is known as the “burn-in”. Moreover, since adjacent samples drawn from the chain (even after burn-in) are highly correlated, we may also skip every several samples to reduced correlation.
designed to be the steady-state probability of the chain (by making sure that detailed balance is satisfied). Note that, however, we have to let the chain to run for a while before the probability distribution converges to the steady-state probability. Thus, samples before the chain reaching equilibrium are discarded. This initial step is known as the “burn-in”. Moreover, since adjacent samples drawn from the chain (even after burn-in) are highly correlated, we may also skip every several samples to reduced correlation.
Metropolis-Hastings
The most well-known MCMC method is the Metropolis-Hastings algorithm. Just as the discussion above, given the distribution ![]() , we want to design Markov chain such that
, we want to design Markov chain such that ![]() satisfies the detailed balance for all states
satisfies the detailed balance for all states ![]() . Given the current state
. Given the current state ![]() , the immediate question is to which state
, the immediate question is to which state ![]() we should transit to. Assuming that
we should transit to. Assuming that ![]() , a simple possibility is just to do a random walk. Essentially perturb
, a simple possibility is just to do a random walk. Essentially perturb ![]() with a zero-mean Gaussian random noise. The problem is that the transition probability
with a zero-mean Gaussian random noise. The problem is that the transition probability ![]() and the “reverse” transition probability
and the “reverse” transition probability ![]() most likely will not satisfy the detailed balance equation
most likely will not satisfy the detailed balance equation ![]() . Without loss of generality, we may have
. Without loss of generality, we may have ![]() . To “balance” the equation, we may reject some of the transition to reduce the probability “flow” on the left hand side. More precisely, let’s denote
. To “balance” the equation, we may reject some of the transition to reduce the probability “flow” on the left hand side. More precisely, let’s denote ![]() . Now, we will randomly reject
. Now, we will randomly reject ![]() of the transition by drawing a uniform
of the transition by drawing a uniform ![]() and only allowing transition if
and only allowing transition if ![]() . And similar adjustment is applied to all transitions (including
. And similar adjustment is applied to all transitions (including ![]() to
to ![]() ). This way, the transition probability from
). This way, the transition probability from ![]() reduces to
reduces to 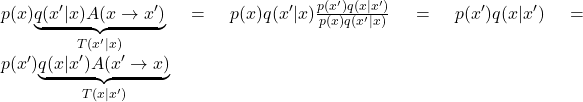 and so the detailed balance equation is satisfied.
and so the detailed balance equation is satisfied.
When the transition probabilities from ![]() to
to ![]() and from
and from ![]() to
to ![]() are equal (i.e.,
are equal (i.e., ![]() ), note that
), note that ![]() just simplifies to
just simplifies to ![]() .
.
Gibbs Sampling
When the state ![]() can be split into multiple component, say
can be split into multiple component, say ![]() . We can transit one component at a time while keeping the rest fixed. For example, we can transit from
. We can transit one component at a time while keeping the rest fixed. For example, we can transit from ![]() to
to ![]() with probability
with probability ![]() . After updating one component, we can update another component in a similar manner until all components are updated. Then, the same procedure can be repeated starting with
. After updating one component, we can update another component in a similar manner until all components are updated. Then, the same procedure can be repeated starting with ![]() . As we continue to update the state, the sample drawn will again converge to
. As we continue to update the state, the sample drawn will again converge to ![]() as the Markov chain reaches equilibrium. This sampling method is known as the Gibbs sampling and can be shown as a special case of Metropolis-Hastings sampling as follows.
as the Markov chain reaches equilibrium. This sampling method is known as the Gibbs sampling and can be shown as a special case of Metropolis-Hastings sampling as follows.
Consider the step when transiting from ![]() to
to ![]() while keeping the rest of components fixed.
while keeping the rest of components fixed. ![]() as defined earlier is
as defined earlier is ![]() . Thus, Gibbs sampling is really Metropolis-Hasting sampling but with all transitions always be accepted.
. Thus, Gibbs sampling is really Metropolis-Hasting sampling but with all transitions always be accepted.
Hamiltonian Monte Carlo (HMC)
The trajectory sampled by the Metropolis-Hasting method is essentially a random walk like a drunk man. But we have the complete information of ![]() and we know how it looks like. Why don’t we leverage the “geometrical” information of
and we know how it looks like. Why don’t we leverage the “geometrical” information of ![]() ?
?
Power of Physics
We definitely can. And recall the Boltzmann distribution ![]() (ignoring temperature here) from statistical physics and we can model any distribution with a Boltzmann distribution with appropriate energy function
(ignoring temperature here) from statistical physics and we can model any distribution with a Boltzmann distribution with appropriate energy function ![]() . Further, we expect lower energy states are more likely to happen than higher energy states as expected.
. Further, we expect lower energy states are more likely to happen than higher energy states as expected.
If we think of ![]() as the potential energy, a “particle” naturally moves towards lower energy state and the excessive energy will convert to kinetic energy as we learn in Newtonian mechanics. Let’s write the total energy as
as the potential energy, a “particle” naturally moves towards lower energy state and the excessive energy will convert to kinetic energy as we learn in Newtonian mechanics. Let’s write the total energy as ![]() , where the potential energy
, where the potential energy ![]() is just
is just ![]() here. (Sorry for the overloading of symbol
here. (Sorry for the overloading of symbol ![]() here,
here, ![]() is commonly used to represent momentum in physics and so we are sticking to that convention here. Please don’t be confuse with the
is commonly used to represent momentum in physics and so we are sticking to that convention here. Please don’t be confuse with the ![]() in
in ![]() .) And the kinetic energy
.) And the kinetic energy ![]() with
with ![]() and
and ![]() being the momentum and the mass, respectively. The total energy,
being the momentum and the mass, respectively. The total energy, ![]() , also known as the Hamiltonian is supposed to be conserved as
, also known as the Hamiltonian is supposed to be conserved as ![]() and
and ![]() naturally vary in the phase space
naturally vary in the phase space ![]() . Therefore,
. Therefore, ![]() .
.
As we know from classical mechanics, ![]() and
and ![]() . For example, let’s consider an object just moving vertically and
. For example, let’s consider an object just moving vertically and ![]() is the height of the object, then
is the height of the object, then ![]() , where
, where ![]() is the gravitational force constant. Then
is the gravitational force constant. Then ![]() with
with ![]() being the gravitational force and
being the gravitational force and ![]() as desired. Moreover, the total energy
as desired. Moreover, the total energy ![]() indeed conserves as
indeed conserves as ![]() and
and ![]() changes as
changes as ![]() .
.
Back to Monte Carlo
Why are we talking all these? Because we can draw samples following natural physical trajectories more efficiently than random walks as in Metropolis-Hastings. Given the distribution of interest ![]() , we again define the Hamiltonian
, we again define the Hamiltonian ![]() . Now, instead of trying to draw samples of
. Now, instead of trying to draw samples of ![]() , we will draw samples of
, we will draw samples of ![]() instead. And
instead. And ![]() . So if we marginalize out the momentum
. So if we marginalize out the momentum ![]() , we get back
, we get back ![]() as desired.
as desired.
And as we samples from the phase space ![]() , rather than random walking in the phase space, we can just follow the flow according to Hamiltonian mechanics as described earlier. For example, as we start from
, rather than random walking in the phase space, we can just follow the flow according to Hamiltonian mechanics as described earlier. For example, as we start from ![]() , we may simulate a short time instace
, we may simulate a short time instace ![]() to
to ![]() with
with ![]() and
and ![]() . One can also update
. One can also update ![]() first and then update
first and then update ![]() . The latter has many different forms and sometimes known as the leapfrog integration. As we apply multiple (
. The latter has many different forms and sometimes known as the leapfrog integration. As we apply multiple (![]() ) leapfrog steps and reach
) leapfrog steps and reach ![]() , we may decide whether to accept the sample as in Metropolis-Hasting by evaluating
, we may decide whether to accept the sample as in Metropolis-Hasting by evaluating ![]() as the transition probabilities are assumed to be the same for both forward and reverse directions. Moreover, if the leapfrog integration is perfect,
as the transition probabilities are assumed to be the same for both forward and reverse directions. Moreover, if the leapfrog integration is perfect, ![]() is supposed to the same as
is supposed to the same as ![]() because of conservation of energy. So we have a high chance of accepting a sample.
because of conservation of energy. So we have a high chance of accepting a sample.
No-U-Turn Sampling (NUTS)
The main challenge of applying HMC is that the algorithm is quite sensitive to the number of leapfrog step ![]() and the step size
and the step size ![]() (more commonly known as
(more commonly known as ![]() ). The goal of NUTS is to automatically select the above two parameters. The main idea is to simulate both forward and backward directions until the algorithm detects reaching a “boundary” and needed to go U-turn. By detecting U-turns, the algorithm can adjust the parameters accordingly. The criterion is simply to check if the momentum starts to turn direction, i.e.,
). The goal of NUTS is to automatically select the above two parameters. The main idea is to simulate both forward and backward directions until the algorithm detects reaching a “boundary” and needed to go U-turn. By detecting U-turns, the algorithm can adjust the parameters accordingly. The criterion is simply to check if the momentum starts to turn direction, i.e., ![]() or
or ![]() , where
, where ![]() and
and ![]() are the two extremes as we go forward and backward in time.
are the two extremes as we go forward and backward in time.
Reference:
- https://en.wikipedia.org/wiki/Hamiltonian_Monte_Carlo
- Mackay, Information Theory, Inference, and Learning Algorithms
- Pattern Recognition and Machine Learning by Bishop
- A Conceptual Introduction to Hamiltonian Monte Carlo
by Michael Betancourt
- The No-U-Turn Sampler: Adaptively Setting Path Lengths in Hamiltonian Monte Carlo
by Matthew D. Hoffman, Andrew Gelman
The three most common graphical models are Bayesian networks (aka directed acyclic graphs), Markov random fields (aka undirected graphs), and factor graphs.
Bayesian networks
A Bayesian network describes the dependency of variables directly represented by the expansion of the conditional probabilities. Take a very simple example with three variables ![]() , and
, and ![]() . If the joint distribution can be represented by
. If the joint distribution can be represented by ![]() . Then, the corresponding Bayesian network will be a three-node graph with
. Then, the corresponding Bayesian network will be a three-node graph with ![]() , and
, and ![]() as vertices. And we have two directed edges one from
as vertices. And we have two directed edges one from ![]() to
to ![]() and another one from
and another one from ![]() to
to ![]() .
.
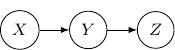
Note that by Bayes rule, the joint probability can be rewritten as ![]() . So the following Bayesian network with directed edges one from
. So the following Bayesian network with directed edges one from ![]() to
to ![]() and another one from
and another one from ![]() to
to ![]() is identical to the earlier one.
is identical to the earlier one.
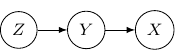
Given ![]() , and
, and ![]() , we may also have an empty graph with no edge at all. This corresponds to the case when
, we may also have an empty graph with no edge at all. This corresponds to the case when ![]() that all three variables are independent as shown below.
that all three variables are independent as shown below.
![]()
We may also have just one edge from ![]() to
to ![]() . This corresponds to the case when
. This corresponds to the case when ![]() , which describes the situation when
, which describes the situation when ![]() is independent of
is independent of ![]() and
and ![]() as shown below.
as shown below.
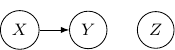
Now, back to the cases with two edges, the ones with two directed edges flowing the same direction will just have the same structure as the example we have earlier. So let’s look at other interesting setups. First, let’s consider the case that both directed edges are coming out of the same variable. For example, we have two directed edges from ![]() to
to ![]() and from
and from ![]() to
to ![]() as shown below.
as shown below.
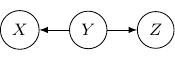
This corresponds to the joint distribution ![]() . So this case is actually the same as the case we have earlier after all. Note that however, this equivalence is not generalizable when we have more variables. For example, say we also have another variable
. So this case is actually the same as the case we have earlier after all. Note that however, this equivalence is not generalizable when we have more variables. For example, say we also have another variable ![]() and an edge from
and an edge from ![]() to
to ![]() .
.
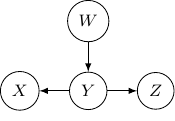
And if we have the direction of the edge ![]() to
to ![]() flipped as below,
flipped as below, ![]() and
and ![]() become independent but the earlier representation does not imply that.
become independent but the earlier representation does not imply that.
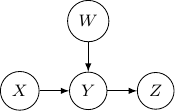
Now, let’s remove ![]() and assume we only have three variables and two edges as described earlier. For all cases we have above (say edges from
and assume we only have three variables and two edges as described earlier. For all cases we have above (say edges from ![]() to
to ![]() and
and ![]() to
to ![]() ), the variables at the two ends
), the variables at the two ends ![]() and
and ![]() are not independent. But they are independent given the variable
are not independent. But they are independent given the variable ![]() in the middle. Be very careful since the situation will be totally flipped as we change the direction of the edge from
in the middle. Be very careful since the situation will be totally flipped as we change the direction of the edge from ![]() to
to ![]() in the following.
in the following.
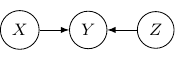
The corresponding joint probability for the above graph is ![]() . We have
. We have ![]() and
and ![]() are independent as
are independent as ![]() . On the other hand, we don’t have
. On the other hand, we don’t have ![]() . And so
. And so ![]() and
and ![]() are not conditional independent given
are not conditional independent given ![]() is observed. The classic example is
is observed. The classic example is ![]() and
and ![]() are two independent binary outcome taking values
are two independent binary outcome taking values ![]() and
and ![]() , where
, where ![]() is the xor operation such that
is the xor operation such that ![]() and
and ![]() . As the xor equation also implies
. As the xor equation also implies ![]() ,
, ![]() is completely determined by
is completely determined by ![]() when
when ![]() is given. Therefore,
is given. Therefore, ![]() is in no way to be independent of
is in no way to be independent of ![]() given
given ![]() . Quite the opposite,
. Quite the opposite, ![]() and
and ![]() are maximally correlated given
are maximally correlated given ![]() .
.
Let’s consider the case with three edges. Note that we can’t have edges forming a loop since Bayesian networks have to be an acyclic graph. A possibility can be having three directed edges one from ![]() to
to ![]() , one from
, one from ![]() to
to ![]() , and the last one from
, and the last one from ![]() to
to ![]() as shown below.
as shown below.
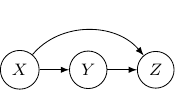
In this case, the joint probability will be ![]() . Note that the joint probability can be directly obtained by Bayes rule and so the graph itself does not assume any dependence/independence structure. The other Bayesian networks with three edges will all be identical and do not imply any independence among variables as well.
. Note that the joint probability can be directly obtained by Bayes rule and so the graph itself does not assume any dependence/independence structure. The other Bayesian networks with three edges will all be identical and do not imply any independence among variables as well.
As we see above, the dependency of variables can be derived from a Bayesian network as the joint probability of the variables can be written down directly. Actually, an important function of all graphical models is to represent such dependency among variables. In terms of Bayesian networks, there is a fancy term known as d-separation which basically refers to the fact that some variables are conditional independent from another given some other variables as can be observed from the Bayesian network. Rather than trying to memorize the rules of d-separation, I think it is much easier to understand the simple three variables examples and realize under what situations that variables are independent or conditionally independent. And for two variables to be conditionally independent of one another, all potential paths of dependency have to be broken down. For example, for the three variables three edges example above (with edges ![]() ,
, ![]() , and
, and ![]() ), observing
), observing ![]() will break the dependency path of
will break the dependency path of ![]() for
for ![]() and
and ![]() . But they are not yet conditionally independent because of the latter path
. But they are not yet conditionally independent because of the latter path ![]() .
.
Let’s consider one last example with four variables ![]() and
and ![]() , and three edges (
, and three edges (![]() ,
, ![]() , and
, and ![]() ) below.
) below.
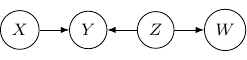
Note that as root nodes, ![]() and
and ![]() are independent. And thus
are independent. And thus ![]() and
and ![]() are independent as well since
are independent as well since ![]() only depends on
only depends on ![]() . On the other hand, if
. On the other hand, if ![]() is observed,
is observed, ![]() and
and ![]() are no longer independent. And thus
are no longer independent. And thus ![]() and
and ![]() are not conditionally independent given
are not conditionally independent given ![]() .
.
Undirected graphs and factor graphs
Compared with Bayesian networks, dependency between variables is much easier to understand. Two variables are independent if they are not connected and two variables are conditionally independent given some variables if the variables are not connected if the vertices of the given variables are removed from the graph.
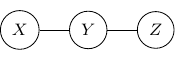
For example, consider a simple undirected graph above with three variables ![]() ,
, ![]() , and
, and ![]() with two edges
with two edges ![]() and
and ![]() . Variables
. Variables ![]() and
and ![]() are then independent given
are then independent given ![]() .
.
By Hammersley-Clifford theorem, the joint probability of any undirected graph models can be represented into the product of factor function of the form ![]() . For example, the joint probability of the above graph can be rewritten as
. For example, the joint probability of the above graph can be rewritten as ![]() with
with ![]() , and
, and ![]() . We can use a bipartite graph to represent the factor product above in the following.
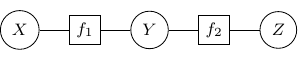
. We can use a bipartite graph to represent the factor product above in the following.
- Represent each factor in the product with a vertex (typically known as factor node and display with a square by convention)
- Represent each random variable with a vertex (typically known as a variable node)
- Connect each factor node to all of its argument with an undirected edge
The graph constructed above is known as a factor graph. With the example described above, we have a factor graph as shown below.
The moralization of Bayesian networks
Consider again the simple Bayesian network with variables ![]() ,
, ![]() , and
, and ![]() , and edges
, and edges ![]() and
and ![]() below.
below.

What should be the corresponding undirected graph to represent this structure?
It is tempting to have the simple undirected graph before with edges ![]() and
and ![]() below.
below.

However, it does not correctly capture the dependency between ![]() and
and ![]() . Recall that when
. Recall that when ![]() is observed or given,
is observed or given, ![]() and
and ![]() are no longer independent. But for the undirected graph above, it exactly captured the opposite. That is
are no longer independent. But for the undirected graph above, it exactly captured the opposite. That is ![]() and
and ![]() are conditionally independent given
are conditionally independent given ![]() . So, to ensure that this conditional independence is not artificially augmented into the model, what we need to do is to add an additional edge
. So, to ensure that this conditional independence is not artificially augmented into the model, what we need to do is to add an additional edge ![]() as shown below.
as shown below.
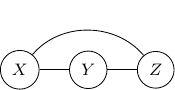
This procedure is sometimes known as moralization. It came for the analogy of a child born out of wedlock and the parents should get married and “moralized”.
Undirected graphs cannot represent all Bayesian networks
Despite the additional edge ![]() , the resulting graph, a fully connected graph with three vertices
, the resulting graph, a fully connected graph with three vertices ![]() ,
, ![]() , and
, and ![]() still does not accurately describe the original Bayesian network. Namely, in the original network,
still does not accurately describe the original Bayesian network. Namely, in the original network, ![]() and
and ![]() are independent but the undirected graph does not capture that.
are independent but the undirected graph does not capture that.
So if either way the model is not a perfect representation, why we bother to moralize the parents anyway? Note that for each edge we added, we reduce the (dependency) assumption behind the model. Solving a relaxed problem with fewer assumptions will not give us the wrong solution. Just maybe will make the problem more difficult to solve. But adding an incorrect assumption that does not exist in the original problem definitely can lead to a very wrong result. So the moralization step is essential when we convert directed to undirected graphs. Make sure you keep all parents in wedlock.
Bayesian networks cannot represent all undirected graphs
Then, does that mean that Bayesian networks are more powerful or have a higher representation power than undirected graphs? Not really also, as there are undirected graphs that cannot be captured by Bayesian networks as well.
Consider undirected graph with four variables ![]() and
and ![]() and four edges
and four edges ![]() ,
, ![]() ,
, ![]() , and
, and ![]() as shown below.
as shown below.
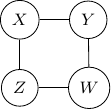
Note that we have conditional independence of ![]() and
and ![]() given
given ![]() and
and ![]() . This conditional independence is captured only by one of the following three Bayesian networks.
. This conditional independence is captured only by one of the following three Bayesian networks.
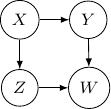
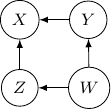
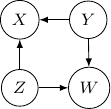
Because of the moralization we discussed earlier, when we convert the above models into undirected graphs, they all require us to add an additional edge between parents ![]() and
and ![]() resulting in the undirected graph below.
resulting in the undirected graph below.
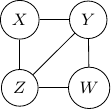
Note that this undirected graph is definitely not the same as the earlier one since it cannot capture the conditional independence between ![]() and
and ![]() given
given ![]() and
and ![]() . In conclusion, no Bayesian network can exactly capture the structure of the square undirected graph above.
. In conclusion, no Bayesian network can exactly capture the structure of the square undirected graph above.