Motivation
While Monte Carlo methods have lots of potential applications, we will just name two here as a motivation:
- Data generation. The generated data can be used for simulation or for visualization purposes.
- Inference. Infer unknown variables from observations.
For the first application, the use of Monte Carlo is rather straight forward. We will assume the model parameters are known and we can sample parameters sequentially with Gibbs sampling as described below. If all conditional distributions can be sampled directly (more explanation below), we can use regular Monte Carlo without the need for MCMC.
For the second application, there is an additional layer of complication as we typically would like to sample from the posterior distribution for efficiency. But often only the likelihood distributions are specified. In that case, we will need to sample from a proposal distribution and MCMC is needed.
Basic Idea of Monte Carlo Methods
Ultimately, almost all Monte Carlo Methods are doing nothing but estimating the expectation of some function ![]() with
with ![]() by
by
![]() ,
,
where the above is guaranteed by the law of large number for sufficiently large ![]() .
.
For example, in the coin-flipping examples in Q1 of HW5, we can estimate the ultimate probability of head by conducting the Monte Carlo experiment and counting the number of head. More precisely, denote ![]() as an indicator function where
as an indicator function where ![]() is 1 when
is 1 when ![]() is head. Then
is head. Then
![]() .
.
The key question here is how we are going to collect samples of ![]() ,
, ![]() . In this coin-flipping setup, the Monte-Carlo simulation is trivial. We can conduct the experiment exactly as in a real setup. That is, first draw a coin from the jar; that corresponds to sample a binary random variable
. In this coin-flipping setup, the Monte-Carlo simulation is trivial. We can conduct the experiment exactly as in a real setup. That is, first draw a coin from the jar; that corresponds to sample a binary random variable ![]() with the specified probability of getting coins
with the specified probability of getting coins ![]() or
or ![]() . Then, based on the outcome of
. Then, based on the outcome of ![]() (i.e., which coin that actually picked), we will draw another binary random variable
(i.e., which coin that actually picked), we will draw another binary random variable ![]() for each coin flip according to the probability of head of the chosen coin.
for each coin flip according to the probability of head of the chosen coin.
In the coin-flipping problem, since we are just drawing binary random variables, we can sample the distribution directly without any issue. But for many continuous distributions except a few special cases, direct sampling them is not possible and more involved sampling techniques are needed as described in the following.
This sequential sampling conditioned on previously specified random variables is generally known as Gibbs sampling. Strictly speaking, it is a form of MCMC as we will show later on. But I think it is more appropriate NOT to consider this simple case as MCMC because there is no convergence issue here as you will see that is generally not the case for MCMC.
Basic Sampling Methods
The key question left is how we can sample data from a distribution. For some standard distributions like Gaussian distribution, we can draw samples directly with some well-developed packages. However, there is no direct way of drawing samples for many regular distributions, not to mention those that do not even have a standard form. There are ways to sample any arbitrary distributions, we will mention a couple of simple ones here.
Rejection Sampling
Probably the simplest sampling method is the rejection sampling. Consider drawing sample ![]() . Select any “sampleable” distribution
. Select any “sampleable” distribution ![]() such that
such that ![]() with some constant
with some constant ![]() . Now, instead of drawing sample from
. Now, instead of drawing sample from ![]() , we will draw from
, we will draw from ![]() instead. However, in order to have the sample appear to have the same distribution of
instead. However, in order to have the sample appear to have the same distribution of ![]() , we will only keep a fraction
, we will only keep a fraction ![]() of
of ![]() whenever
whenever ![]() is drawn and discard the rest. To do this, we simply sample a
is drawn and discard the rest. To do this, we simply sample a ![]() from
from ![]() uniformly after each
uniformly after each ![]() sampled. And keep the current
sampled. And keep the current ![]() only if
only if ![]() .
.
Note that in Q4 of HW5, we are essentially doing some form of rejection sampling. Draw the samples from the prior and the likelihood distributions, and then only accept samples that fit the observations. Rejection sampling is simple but it can be quite inefficient. For example, if the current estimates of variables used in sampling are far from the actual values, the sampled outcome most likely will not match well with the observations and we have to reject lots of samples. That’s why other sampling techniques are needed.
Importance Sampling
Rejection sampling is generally very inefficient as a large number of samples can be discarded. If we only care about computing the expection of some function, then we may not need to discard any sample but adjust the weight of each sample instead. Note that
![Rendered by QuickLaTeX.com E_{X\sim p(x)}[f(X)]=\int f(x) p(x) dx = \int \left[f(x)\frac{p(x)}{q(x)}\right] q(x) dx= E_{X\sim q(x)}\left[f(X)\frac{p(X)}{q(X)}\right]](https://outliip.org/wp-content/ql-cache/quicklatex.com-d44ddc9ce7e912f6d9872ce5cced50c1_l3.png) .
.
Thus, we can estimate the expectation by drawing samples from ![]() and compute weighted average of
and compute weighted average of ![]() instead. And the corresponding weights are
instead. And the corresponding weights are ![]() .
.
Even though we can now utilize all samples, importance sampling has two concerns.
- Unlike rejection sampling, we do not directly draw samples with the desired distribution. So we can use those samples to do other things rather than computing expectations.
- The variance of the estimate can be highly sensitive with the choice of
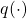 . In particular, since the variance of the estimate is
. In particular, since the variance of the estimate is ![Rendered by QuickLaTeX.com \frac{1}{N}E\left[ f(X)\frac{p(X)}{q(X)}\right]](https://outliip.org/wp-content/ql-cache/quicklatex.com-8dbe52483531c01ca6f87a0182b0ba52_l3.png) , the variance will be especially large if a more probable region in
, the variance will be especially large if a more probable region in 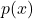 is not covered well by
is not covered well by 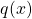 , i.e., we have extensive region where
, i.e., we have extensive region where 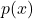 large but
large but 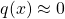 .
.
Markov Chain Monte Carlo
Instead of sampling from ![]() directly, Markov chain Monte Carlo (MCMC) methods try to sample from a Markov chain (essentially a probabilistic state model). Probably the two most important properties of the Markov chain are irreducible and aperiodic. We say a Markov chain is irreducible if we can reach any single state to any other state. And we say a Markov chain is periodic if there exist two states such that one state can reach the other state only in a multiple of
directly, Markov chain Monte Carlo (MCMC) methods try to sample from a Markov chain (essentially a probabilistic state model). Probably the two most important properties of the Markov chain are irreducible and aperiodic. We say a Markov chain is irreducible if we can reach any single state to any other state. And we say a Markov chain is periodic if there exist two states such that one state can reach the other state only in a multiple of ![]() steps with
steps with ![]() . If a Markov chain is not periodic, we say it is aperiodic. Under the above two conditions (aperiodic and irreducible), regardless of the initial state, the distribution of states will converge to the steady-state probability distribution asymptotically as time goes to infinity.
. If a Markov chain is not periodic, we say it is aperiodic. Under the above two conditions (aperiodic and irreducible), regardless of the initial state, the distribution of states will converge to the steady-state probability distribution asymptotically as time goes to infinity.
Consider any two connected states with transition probabilities ![]() (from
(from ![]() to
to ![]() ) and
) and ![]() (from
(from ![]() to
to ![]() ). We say the detailed balance equations are satisfied if
). We say the detailed balance equations are satisfied if ![]() . Note that if detailed balance are satisfied among all states,
. Note that if detailed balance are satisfied among all states, ![]() has to be the steady state probability of state
has to be the steady state probability of state ![]() . Because the probability “flux” going out from
. Because the probability “flux” going out from ![]() to
to ![]() is exactly canceled by the “flux” coming in from
is exactly canceled by the “flux” coming in from ![]() to
to ![]() when the chain reaches this equalibrium.
when the chain reaches this equalibrium.
With the discussion above, we see that one can sample ![]() if we can create a Markov chain with
if we can create a Markov chain with ![]() designed to be the steady-state probability of the chain (by making sure that detailed balance is satisfied). Note that, however, we have to let the chain to run for a while before the probability distribution converges to the steady-state probability. Thus, samples before the chain reaching equilibrium are discarded. This initial step is known as the “burn-in”. Moreover, since adjacent samples drawn from the chain (even after burn-in) are highly correlated, we may also skip every several samples to reduced correlation.
designed to be the steady-state probability of the chain (by making sure that detailed balance is satisfied). Note that, however, we have to let the chain to run for a while before the probability distribution converges to the steady-state probability. Thus, samples before the chain reaching equilibrium are discarded. This initial step is known as the “burn-in”. Moreover, since adjacent samples drawn from the chain (even after burn-in) are highly correlated, we may also skip every several samples to reduced correlation.
Metropolis-Hastings
The most well-known MCMC method is the Metropolis-Hastings algorithm. Just as the discussion above, given the distribution ![]() , we want to design Markov chain such that
, we want to design Markov chain such that ![]() satisfies the detailed balance for all states
satisfies the detailed balance for all states ![]() . Given the current state
. Given the current state ![]() , the immediate question is to which state
, the immediate question is to which state ![]() we should transit to. Assuming that
we should transit to. Assuming that ![]() , a simple possibility is just to do a random walk. Essentially perturb
, a simple possibility is just to do a random walk. Essentially perturb ![]() with a zero-mean Gaussian random noise. The problem is that the transition probability
with a zero-mean Gaussian random noise. The problem is that the transition probability ![]() and the “reverse” transition probability
and the “reverse” transition probability ![]() most likely will not satisfy the detailed balance equation
most likely will not satisfy the detailed balance equation ![]() . Without loss of generality, we may have
. Without loss of generality, we may have ![]() . To “balance” the equation, we may reject some of the transition to reduce the probability “flow” on the left hand side. More precisely, let’s denote
. To “balance” the equation, we may reject some of the transition to reduce the probability “flow” on the left hand side. More precisely, let’s denote ![]() . Now, we will randomly reject
. Now, we will randomly reject ![]() of the transition by drawing a uniform
of the transition by drawing a uniform ![]() and only allowing transition if
and only allowing transition if ![]() . And similar adjustment is applied to all transitions (including
. And similar adjustment is applied to all transitions (including ![]() to
to ![]() ). This way, the transition probability from
). This way, the transition probability from ![]() reduces to
reduces to 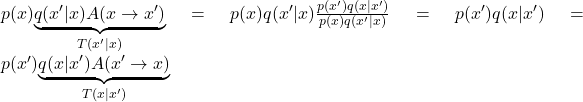 and so the detailed balance equation is satisfied.
and so the detailed balance equation is satisfied.
When the transition probabilities from ![]() to
to ![]() and from
and from ![]() to
to ![]() are equal (i.e.,
are equal (i.e., ![]() ), note that
), note that ![]() just simplifies to
just simplifies to ![]() .
.
Gibbs Sampling
When the state ![]() can be split into multiple component, say
can be split into multiple component, say ![]() . We can transit one component at a time while keeping the rest fixed. For example, we can transit from
. We can transit one component at a time while keeping the rest fixed. For example, we can transit from ![]() to
to ![]() with probability
with probability ![]() . After updating one component, we can update another component in a similar manner until all components are updated. Then, the same procedure can be repeated starting with
. After updating one component, we can update another component in a similar manner until all components are updated. Then, the same procedure can be repeated starting with ![]() . As we continue to update the state, the sample drawn will again converge to
. As we continue to update the state, the sample drawn will again converge to ![]() as the Markov chain reaches equilibrium. This sampling method is known as the Gibbs sampling and can be shown as a special case of Metropolis-Hastings sampling as follows.
as the Markov chain reaches equilibrium. This sampling method is known as the Gibbs sampling and can be shown as a special case of Metropolis-Hastings sampling as follows.
Consider the step when transiting from ![]() to
to ![]() while keeping the rest of components fixed.
while keeping the rest of components fixed. ![]() as defined earlier is
as defined earlier is ![]() . Thus, Gibbs sampling is really Metropolis-Hasting sampling but with all transitions always be accepted.
. Thus, Gibbs sampling is really Metropolis-Hasting sampling but with all transitions always be accepted.
Hamiltonian Monte Carlo (HMC)
The trajectory sampled by the Metropolis-Hasting method is essentially a random walk like a drunk man. But we have the complete information of ![]() and we know how it looks like. Why don’t we leverage the “geometrical” information of
and we know how it looks like. Why don’t we leverage the “geometrical” information of ![]() ?
?
Power of Physics
We definitely can. And recall the Boltzmann distribution ![]() (ignoring temperature here) from statistical physics and we can model any distribution with a Boltzmann distribution with appropriate energy function
(ignoring temperature here) from statistical physics and we can model any distribution with a Boltzmann distribution with appropriate energy function ![]() . Further, we expect lower energy states are more likely to happen than higher energy states as expected.
. Further, we expect lower energy states are more likely to happen than higher energy states as expected.
If we think of ![]() as the potential energy, a “particle” naturally moves towards lower energy state and the excessive energy will convert to kinetic energy as we learn in Newtonian mechanics. Let’s write the total energy as
as the potential energy, a “particle” naturally moves towards lower energy state and the excessive energy will convert to kinetic energy as we learn in Newtonian mechanics. Let’s write the total energy as ![]() , where the potential energy
, where the potential energy ![]() is just
is just ![]() here. (Sorry for the overloading of symbol
here. (Sorry for the overloading of symbol ![]() here,
here, ![]() is commonly used to represent momentum in physics and so we are sticking to that convention here. Please don’t be confuse with the
is commonly used to represent momentum in physics and so we are sticking to that convention here. Please don’t be confuse with the ![]() in
in ![]() .) And the kinetic energy
.) And the kinetic energy ![]() with
with ![]() and
and ![]() being the momentum and the mass, respectively. The total energy,
being the momentum and the mass, respectively. The total energy, ![]() , also known as the Hamiltonian is supposed to be conserved as
, also known as the Hamiltonian is supposed to be conserved as ![]() and
and ![]() naturally vary in the phase space
naturally vary in the phase space ![]() . Therefore,
. Therefore, ![]() .
.
As we know from classical mechanics, ![]() and
and ![]() . For example, let’s consider an object just moving vertically and
. For example, let’s consider an object just moving vertically and ![]() is the height of the object, then
is the height of the object, then ![]() , where
, where ![]() is the gravitational force constant. Then
is the gravitational force constant. Then ![]() with
with ![]() being the gravitational force and
being the gravitational force and ![]() as desired. Moreover, the total energy
as desired. Moreover, the total energy ![]() indeed conserves as
indeed conserves as ![]() and
and ![]() changes as
changes as ![]() .
.
Back to Monte Carlo
Why are we talking all these? Because we can draw samples following natural physical trajectories more efficiently than random walks as in Metropolis-Hastings. Given the distribution of interest ![]() , we again define the Hamiltonian
, we again define the Hamiltonian ![]() . Now, instead of trying to draw samples of
. Now, instead of trying to draw samples of ![]() , we will draw samples of
, we will draw samples of ![]() instead. And
instead. And ![]() . So if we marginalize out the momentum
. So if we marginalize out the momentum ![]() , we get back
, we get back ![]() as desired.
as desired.
And as we samples from the phase space ![]() , rather than random walking in the phase space, we can just follow the flow according to Hamiltonian mechanics as described earlier. For example, as we start from
, rather than random walking in the phase space, we can just follow the flow according to Hamiltonian mechanics as described earlier. For example, as we start from ![]() , we may simulate a short time instace
, we may simulate a short time instace ![]() to
to ![]() with
with ![]() and
and ![]() . One can also update
. One can also update ![]() first and then update
first and then update ![]() . The latter has many different forms and sometimes known as the leapfrog integration. As we apply multiple (
. The latter has many different forms and sometimes known as the leapfrog integration. As we apply multiple (![]() ) leapfrog steps and reach
) leapfrog steps and reach ![]() , we may decide whether to accept the sample as in Metropolis-Hasting by evaluating
, we may decide whether to accept the sample as in Metropolis-Hasting by evaluating ![]() as the transition probabilities are assumed to be the same for both forward and reverse directions. Moreover, if the leapfrog integration is perfect,
as the transition probabilities are assumed to be the same for both forward and reverse directions. Moreover, if the leapfrog integration is perfect, ![]() is supposed to the same as
is supposed to the same as ![]() because of conservation of energy. So we have a high chance of accepting a sample.
because of conservation of energy. So we have a high chance of accepting a sample.
No-U-Turn Sampling (NUTS)
The main challenge of applying HMC is that the algorithm is quite sensitive to the number of leapfrog step ![]() and the step size
and the step size ![]() (more commonly known as
(more commonly known as ![]() ). The goal of NUTS is to automatically select the above two parameters. The main idea is to simulate both forward and backward directions until the algorithm detects reaching a “boundary” and needed to go U-turn. By detecting U-turns, the algorithm can adjust the parameters accordingly. The criterion is simply to check if the momentum starts to turn direction, i.e.,
). The goal of NUTS is to automatically select the above two parameters. The main idea is to simulate both forward and backward directions until the algorithm detects reaching a “boundary” and needed to go U-turn. By detecting U-turns, the algorithm can adjust the parameters accordingly. The criterion is simply to check if the momentum starts to turn direction, i.e., ![]() or
or ![]() , where
, where ![]() and
and ![]() are the two extremes as we go forward and backward in time.
are the two extremes as we go forward and backward in time.
Reference:
- https://en.wikipedia.org/wiki/Hamiltonian_Monte_Carlo
- Mackay, Information Theory, Inference, and Learning Algorithms
- Pattern Recognition and Machine Learning by Bishop
- A Conceptual Introduction to Hamiltonian Monte Carlo
by Michael Betancourt
- The No-U-Turn Sampler: Adaptively Setting Path Lengths in Hamiltonian Monte Carlo
by Matthew D. Hoffman, Andrew Gelman