November 2020 – OU-Tulsa Lab of Image and Information Processing

Bayesian networks, Markov random fields, and factor graphs

November 17, 2020 by samuel.cheng@ou.edu - No comments

The three most common graphical models are Bayesian networks (aka directed acyclic graphs), Markov random fields (aka undirected graphs), and factor graphs.

Bayesian networks

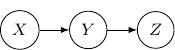
A Bayesian network describes the dependency of variables directly represented by the expansion of the conditional probabilities. Take a very simple example with three variables $X, Y$ , and $Z$ . If the joint distribution can be represented by $p(x) p(y|x) p(z|y)$ . Then, the corresponding Bayesian network will be a three-node graph with $X, Y$ , and $Z$ as vertices. And we have two directed edges one from $X$ to $Y$ and another one from $Y$ to $Z$ .

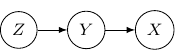
Note that by Bayes rule, the joint probability can be rewritten as $p(z) p(y|z) p(x|y)$ . So the following Bayesian network with directed edges one from $Z$ to $Y$ and another one from $Y$ to $X$ is identical to the earlier one.

Given $X, Y$ , and $Z$ , we may also have an empty graph with no edge at all. This corresponds to the case when $p(x,y,z)=p(x)p(y)p(z)$ that all three variables are independent as shown below.

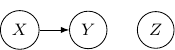
We may also have just one edge from $x$ to $y$ . This corresponds to the case when $p(x,y,z)=p(x)p(y|x) p(z)$ , which describes the situation when $Z$ is independent of $X$ and $Y$ as shown below.

Now, back to the cases with two edges, the ones with two directed edges flowing the same direction will just have the same structure as the example we have earlier. So let’s look at other interesting setups. First, let’s consider the case that both directed edges are coming out of the same variable. For example, we have two directed edges from $Y$ to $X$ and from $Y$ to $Z$ as shown below.

This corresponds to the joint distribution $p(x,y,z)=p(y)p(x|y)p(z|y)=p(x)p(y|x)p(z|y)$ . So this case is actually the same as the case we have earlier after all. Note that however, this equivalence is not generalizable when we have more variables. For example, say we also have another variable $W$ and an edge from $W$ to $Y$ .

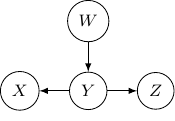
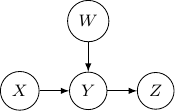
And if we have the direction of the edge $Y$ to $X$ flipped as below, $W$ and $X$ become independent but the earlier representation does not imply that.

Now, let’s remove $W$ and assume we only have three variables and two edges as described earlier. For all cases we have above (say edges from $X$ to $Y$ and $Y$ to $Z$ ), the variables at the two ends $X$ and $Z$ are not independent. But they are independent given the variable $Y$ in the middle. Be very careful since the situation will be totally flipped as we change the direction of the edge from $Y$ to $Z$ in the following.

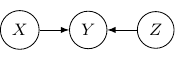
The corresponding joint probability for the above graph is $p(x,y,z)=p(x) p(z) p(y|x,z)$ . We have $X$ and $Z$ are independent as $p(x,z)=\sum_z p(x,y,z)=\sum_z p(x)p(z)p(y|x,z)=p(x)p(z)$ . On the other hand, we don’t have $p(x,z|y)=p(x|y)p(z|y)$ . And so $X$ and $Z$ are not conditional independent given $Y$ is observed. The classic example is $X$ and $Z$ are two independent binary outcome taking values $\{0,1\}$ and $Y = X \oplus Z$ , where $\oplus$ is the xor operation such that $1\oplus 1=0\oplus 0=0$ and $0\oplus 1=1 \oplus 0=1$ . As the xor equation also implies $X =Z \oplus Y$ , $X$ is completely determined by $Z$ when $Y$ is given. Therefore, $X$ is in no way to be independent of $Z$ given $Y$ . Quite the opposite, $X$ and $Z$ are maximally correlated given $Y$ .

Let’s consider the case with three edges. Note that we can’t have edges forming a loop since Bayesian networks have to be an acyclic graph. A possibility can be having three directed edges one from $X$ to $Y$ , one from $Y$ to $Z$ , and the last one from $X$ to $Z$ as shown below.

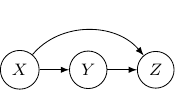
In this case, the joint probability will be $p(x,y,z)=p(x)p(y|x)p(z|x,y)$ . Note that the joint probability can be directly obtained by Bayes rule and so the graph itself does not assume any dependence/independence structure. The other Bayesian networks with three edges will all be identical and do not imply any independence among variables as well.

As we see above, the dependency of variables can be derived from a Bayesian network as the joint probability of the variables can be written down directly. Actually, an important function of all graphical models is to represent such dependency among variables. In terms of Bayesian networks, there is a fancy term known as d-separation which basically refers to the fact that some variables are conditional independent from another given some other variables as can be observed from the Bayesian network. Rather than trying to memorize the rules of d-separation, I think it is much easier to understand the simple three variables examples and realize under what situations that variables are independent or conditionally independent. And for two variables to be conditionally independent of one another, all potential paths of dependency have to be broken down. For example, for the three variables three edges example above (with edges $X\rightarrow Y$ , $Y\rightarrow Z$ , and $X\rightarrow Z$ ), observing $Y$ will break the dependency path of $X\rightarrow Y\rightarrow Z$ for $X$ and $Z$ . But they are not yet conditionally independent because of the latter path $X\rightarrow Z$ .

Let’s consider one last example with four variables $X,Y,Z$ and $W$ , and three edges ( $X\rightarrow Y$ , $Z\rightarrow Y$ , and $Z\rightarrow W$ ) below.

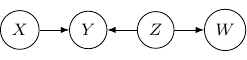
Note that as root nodes, $X$ and $Z$ are independent. And thus $X$ and $W$ are independent as well since $W$ only depends on $Z$ . On the other hand, if $Y$ is observed, $X$ and $Z$ are no longer independent. And thus $X$ and $W$ are not conditionally independent given $Y$ .

Undirected graphs and factor graphs

Compared with Bayesian networks, dependency between variables is much easier to understand. Two variables are independent if they are not connected and two variables are conditionally independent given some variables if the variables are not connected if the vertices of the given variables are removed from the graph.

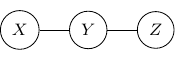
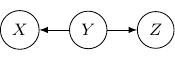
For example, consider a simple undirected graph above with three variables $X$ , $Y$ , and $Z$ with two edges $X - Y$ and $Y-Z$ . Variables $X$ and $Z$ are then independent given $Y$ .

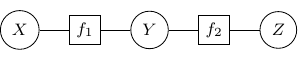
By Hammersley-Clifford theorem, the joint probability of any undirected graph models can be represented into the product of factor function of the form $\prod_{\bf i} \phi_i ({\bf x}_i)$ . For example, the joint probability of the above graph can be rewritten as $f_1(x,y)f_2(y,z)$ with $f_1(x,y)=p(x|y)$ , and $f_2(y,z)=p(y)p(z|y)$ . We can use a bipartite graph to represent the factor product above in the following.

Represent each factor in the product with a vertex (typically known as factor node and display with a square by convention)
Represent each random variable with a vertex (typically known as a variable node)
Connect each factor node to all of its argument with an undirected edge

The graph constructed above is known as a factor graph. With the example described above, we have a factor graph as shown below.

The moralization of Bayesian networks

Consider again the simple Bayesian network with variables $X$ , $Y$ , and $Z$ , and edges $X\rightarrow Y$ and $Z\rightarrow Y$ below.

What should be the corresponding undirected graph to represent this structure?

It is tempting to have the simple undirected graph before with edges $X - Y$ and $Y-Z$ below.

However, it does not correctly capture the dependency between $X$ and $Z$ . Recall that when $Y$ is observed or given, $X$ and $Z$ are no longer independent. But for the undirected graph above, it exactly captured the opposite. That is $X$ and $Z$ are conditionally independent given $Y$ . So, to ensure that this conditional independence is not artificially augmented into the model, what we need to do is to add an additional edge $X - Z$ as shown below.

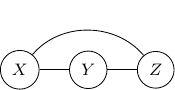
This procedure is sometimes known as moralization. It came for the analogy of a child born out of wedlock and the parents should get married and “moralized”.

Undirected graphs cannot represent all Bayesian networks

Despite the additional edge $X-Z$ , the resulting graph, a fully connected graph with three vertices $X$ , $Y$ , and $Z$ still does not accurately describe the original Bayesian network. Namely, in the original network, $X$ and $Z$ are independent but the undirected graph does not capture that.

So if either way the model is not a perfect representation, why we bother to moralize the parents anyway? Note that for each edge we added, we reduce the (dependency) assumption behind the model. Solving a relaxed problem with fewer assumptions will not give us the wrong solution. Just maybe will make the problem more difficult to solve. But adding an incorrect assumption that does not exist in the original problem definitely can lead to a very wrong result. So the moralization step is essential when we convert directed to undirected graphs. Make sure you keep all parents in wedlock.

Bayesian networks cannot represent all undirected graphs

Then, does that mean that Bayesian networks are more powerful or have a higher representation power than undirected graphs? Not really also, as there are undirected graphs that cannot be captured by Bayesian networks as well.

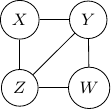
Consider undirected graph with four variables $X, Y, Z,$ and $W$ and four edges $X-Y$ , $Y-W$ , $Z-W$ , and $Z-X$ as shown below.

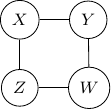
Note that we have conditional independence of $X$ and $W$ given $Y$ and $Z$ . This conditional independence is captured only by one of the following three Bayesian networks.

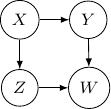
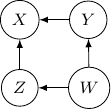
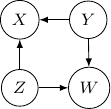
Because of the moralization we discussed earlier, when we convert the above models into undirected graphs, they all require us to add an additional edge between parents $Y$ and $Z$ resulting in the undirected graph below.

Note that this undirected graph is definitely not the same as the earlier one since it cannot capture the conditional independence between $Y$ and $Z$ given $W$ and $X$ . In conclusion, no Bayesian network can exactly capture the structure of the square undirected graph above.

teaching

Tossing unknown biased coin

November 14, 2020 by samuel.cheng@ou.edu - No comments

Assume that there are two biased coins. Coin A heavily biased towards head with the probability of head equal to 0.9. And Coin B is heavily biased towards tail with the probability of tail equal to 0.9. Now, we randomly and equally likely select one of the coins and toss it twice. Let’s call the outcome $Y_1$ and $Y_2$ . Now, the question is, what is the mutual information between $Y_1$ and $Y_2$ ?

I put a similar question as above in a midterm, and I didn’t expect to stumble the entire class.

All students thought that the mutual information $I(Y_1;Y_2)=0$ because the two outcomes are independent. When we toss a coin sequentially, the outcomes are supposed to be independent, right? Yes, but that is only when we know what coin we are tossing.

Think intuitively with the above example. If we didn’t toss the coin twice, but toss it ten times and got ten heads. What do we expect the outcome to be if we toss it another time?

I think an intelligent guess should be another head. Because given the ten heads we got earlier, it has a very high chance that the picked coin is Coin A. And so the next toss is very likely to be the head as well.

Now, the same argument holds when we are back to the original setup. When the first toss is head, the second toss is likely to be head as well. So $Y_1$ and $Y_2$ are in no way to be independent.

So what is $I(Y_1; Y_2)$ ?

$I(Y_1;Y_2)=H(Y_1)+H(Y_2)-H(Y_1,Y_2)=2H(Y_1)-H(Y_1,Y_2)$

Let’s compute $H(Y_1)$ and $H(Y_1,Y_2)$ .

Denote $X$ as the coin that we pick.

$Pr(Y_1=H)=Pr(X=A)0.9+Pr(X=B)0.1=0.5$

So $H(Y_1)=H(0.5)=1$ bit.

Now, for $H(Y_1,Y_2)$ , note that

$p_{Y_1,Y_2}(H,H)=Pr(X=A)(0.9\cdot 0.9) + Pr(X=B)(0.1\cdot 0.1)=0.41$

$p_{Y_1,Y_2}(T,T)=Pr(X=A)(0.1\cdot 0.1)+Pr(X=B)(0.9\cdot 0.9)=0.41$

$p_{Y_1,Y_2}(T,H)=p_{Y_1,Y_2}(H,T)=Pr(X=A)(0.1\cdot 0.9)+Pr(X=B)(0.9\cdot 0.1)=0.09$

Therefore, $H(Y_1,Y_2)=H([0.41,0.41,0.09,0.09])=1.68$ bit.

So $I(Y_1;Y_2)=H(Y_1)+H(Y_2)-H(Y_1,Y_2)=0.32$ bit.

Note that this is an example that variables are conditional independent but not independent. More precisely, we have $Y_1 \not\bot Y_2$ but $Y_1 \bot Y_2|X$ .

Probability education trap

I wondered a little bit why none of my students could answer the above question. I blame a trap that is embedded in most elementary probability courses. We were always introduced with a consecutive coin tossing or dice throwing example with each subsequent event to be independent of the earlier event. In those examples, we always assume that the probabilities of getting all outcomes are known but this assumption was never emphasized. As we see in the above example, even each subsequent tossing or throwing is independent relative to the current coin or the current dice, overall those events are not independent when the statistics behind the coin and dice are not known.

Actually, this also makes some “pseudo-science” not really that non-scientific after all. For example, we all tend to believe that the gender of a newborn is close to random and hence unpredictable. But what if there is some hidden variable that affects the gender of a newborn. And that factor may have a strong bias towards one gender over another. Then, it probably is not really that unlikely for someone to have five consecutive girls or six consecutive sons. Of course, I also tend to believe that the probability of a newborn to be a boy or a girl is very close to one half. A less extreme example may occur at the casino. If we believe that the odd from each lottery machine in a casino is not so perfectly tune (before the digital age, that is probably much more likely), then there is a chance that some machine has a higher average reward than another one. Then, a gambler trying to select a lottery machine to play is an essential strategy to win and is not really superstition after all. Of course, this is just the multi-armed bandit problem.

teaching

Independence and conditional independence

by samuel.cheng@ou.edu - No comments

Independence and conditional independence are one of the most basic concepts in probabilities. Two random variables are independent, as the term suggested, if the outcome of one variable should not affect the outcome of another. Mathematically, two variables $X$ and $Y$ are independent if

$p(x,y) = p(x) p(y)$ for any outcome $x$ for variable $X$ and outcome $y$ for variable $Y$ . And we often indicate this independece by $X \bot Y$ .

Let’s inspect this definition more carefully, given $Y=y$ and by Bayes’ rule, the probability of $X=x$ is

$Pr(X=x|Y=y)=\frac{p(x,y)}{p(y)}= \frac{p(x)p(y)}{p(y)}=p(x)$ . Indeed the probability does not depend on the outcome of $Y$ and so $X$ and $Y$ are independent.

Similarly, when we say $X$ and $Y$ are conditionally independent given $Z$ , it means that knowing $Z$ , $X$ and $Y$ become independent. Note that $X$ and $Y$ do not need to be independent to start with. Many students have the misconceptions that independence implies conditional independence, or vice versa. The fact is that they are completely unrelated concepts. We can easily find examples that variables are independent but not conditional independent and vice versa. And also examples that variables are both independent and conditional independent. And of course cases when neither independence is satisfied.

Mathematically, we denote the independence by $X \bot Y|Z$ , and we have

$p(x,y|z)=p(x|z)p(y|z)$ for any $x, y$ , and $z$ .

Note that the definition above implies that $p(x|y,z)=\frac{p(x,y|z)}{p(y|z)}=p(x|z)$ . Hence, indeed if we are given $z$ , the probability of $X=x$ does not dependent on the outcome of $Y$ . So it depicts well the conditional independence that we anticipated.

M	T	W	T	F	S	S
						1
2	3	4	5	6	7	8
9	10	11	12	13	14	15
16	17	18	19	20	21	22
23	24	25	26	27	28	29
30

Month: November 2020