Assume that there are two biased coins. Coin A heavily biased towards head with the probability of head equal to 0.9. And Coin B is heavily biased towards tail with the probability of tail equal to 0.9. Now, we randomly and equally likely select one of the coins and toss it twice. Let’s call the outcome ![]() and
and ![]() . Now, the question is, what is the mutual information between
. Now, the question is, what is the mutual information between ![]() and
and ![]() ?
?
I put a similar question as above in a midterm, and I didn’t expect to stumble the entire class.
All students thought that the mutual information ![]() because the two outcomes are independent. When we toss a coin sequentially, the outcomes are supposed to be independent, right? Yes, but that is only when we know what coin we are tossing.
because the two outcomes are independent. When we toss a coin sequentially, the outcomes are supposed to be independent, right? Yes, but that is only when we know what coin we are tossing.
Think intuitively with the above example. If we didn’t toss the coin twice, but toss it ten times and got ten heads. What do we expect the outcome to be if we toss it another time?
I think an intelligent guess should be another head. Because given the ten heads we got earlier, it has a very high chance that the picked coin is Coin A. And so the next toss is very likely to be the head as well.
Now, the same argument holds when we are back to the original setup. When the first toss is head, the second toss is likely to be head as well. So ![]() and
and ![]() are in no way to be independent.
are in no way to be independent.
So what is ![]() ?
?
![]()
Let’s compute 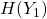 and
and 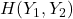 .
.
Denote ![]() as the coin that we pick.
as the coin that we pick.
![]()
So ![]() bit.
bit.
Now, for ![]() , note that
, note that
![]()
![]()
![]()
Therefore, ![]() bit.
bit.
So 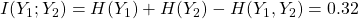 bit.
bit.
Note that this is an example that variables are conditional independent but not independent. More precisely, we have ![]() but
but ![]() .
.
Probability education trap
I wondered a little bit why none of my students could answer the above question. I blame a trap that is embedded in most elementary probability courses. We were always introduced with a consecutive coin tossing or dice throwing example with each subsequent event to be independent of the earlier event. In those examples, we always assume that the probabilities of getting all outcomes are known but this assumption was never emphasized. As we see in the above example, even each subsequent tossing or throwing is independent relative to the current coin or the current dice, overall those events are not independent when the statistics behind the coin and dice are not known.
Actually, this also makes some “pseudo-science” not really that non-scientific after all. For example, we all tend to believe that the gender of a newborn is close to random and hence unpredictable. But what if there is some hidden variable that affects the gender of a newborn. And that factor may have a strong bias towards one gender over another. Then, it probably is not really that unlikely for someone to have five consecutive girls or six consecutive sons. Of course, I also tend to believe that the probability of a newborn to be a boy or a girl is very close to one half. A less extreme example may occur at the casino. If we believe that the odd from each lottery machine in a casino is not so perfectly tune (before the digital age, that is probably much more likely), then there is a chance that some machine has a higher average reward than another one. Then, a gambler trying to select a lottery machine to play is an essential strategy to win and is not really superstition after all. Of course, this is just the multi-armed bandit problem.