Self-supervised learning from Meta claimed to beat state of the art without fine tuning.
Category: Deep Learning
A, B, and C are to fight a three-cornered pistol duel. All know that A’s chance of hitting his target is 0.3, C’s is 0.5, and B never misses. They are to fire at their choice of target in succession in the order A, B, C, cyclically (but a hit man loses further turns and is no longer shot at) until only one man is left unhit. What should A’s strategy be?
A’s best strategy in this three-cornered pistol duel is to intentionally miss his first shot. Here’s the reasoning behind this strategy:
- If A shoots and hits either B or C, then the remaining two players will fight a regular duel. Since B never misses, B would win against either A or C. So, eliminating one player is not advantageous for A.
- If A intentionally misses his first shot, then B and C will have their turns. B knows that C is a more dangerous opponent because C’s probability of hitting the target is 0.5, while A’s is only 0.3. Therefore, B should target C, and if B hits C, the duel becomes a one-on-one match between A and B.
In the one-on-one duel, A has the first shot against B. A has a 0.3 chance of hitting B and surviving the duel. If A misses, B will shoot and win since B never misses. Therefore, A’s overall chance of winning the duel is 0.3 when he intentionally misses his first shot, which is better than the alternative of targeting either B or C in the beginning.
The answer is correct
coupon in cereal boxes are numbered 1 to 5, and a set of one of each is required for a price. with one coupon per box, how many boxes on the average are required to make a complete set?
This problem can be solved using the concept of expected value. We can compute the expected number of boxes required to complete a set of coupons numbered 1 to 5 by considering the average number of boxes needed to collect each subsequent unique coupon.
Let’s break down the process of collecting a complete set of coupons:
- The first coupon: Since you don’t have any coupons yet, you are guaranteed to get a unique coupon in the first box. The expected number of boxes to get the first coupon is 1.
- The second coupon: The probability of getting a new coupon is 4/5 (since there are 4 new coupons you don’t have yet). The expected number of boxes to get the second coupon is 1 / (4/5) = 5/4.
- The third coupon: The probability of getting a new coupon is 3/5 (since there are 3 new coupons you don’t have yet). The expected number of boxes to get the third coupon is 1 / (3/5) = 5/3.
- The fourth coupon: The probability of getting a new coupon is 2/5 (since there are 2 new coupons you don’t have yet). The expected number of boxes to get the fourth coupon is 1 / (2/5) = 5/2.
- The fifth coupon: The probability of getting the last coupon is 1/5 (since there is only 1 new coupon you don’t have yet). The expected number of boxes to get the fifth coupon is 1 / (1/5) = 5.
To find the expected number of boxes needed to complete the set, we add the expected number of boxes for each unique coupon:
Expected number of boxes = 1 + 5/4 + 5/3 + 5/2 + 5 = 1 + 1.25 + 1.67 + 2.5 + 5 ≈ 11.42
On average, you would need to buy approximately 11.42 boxes to collect a complete set of coupons numbered 1 to 5.
This answer is correct again.
A 1-meter stick is randomly broken into 4 pieces, what is the expected length of the shortest piece?
To find the expected length of the shortest piece when a 1-meter stick is randomly broken into 4 pieces, we can use the concept of order statistics.
Let’s represent the break points on the stick as X1, X2, and X3, which are random variables uniformly distributed between 0 and 1. We can arrange these break points in ascending order, such that X1 <= X2 <= X3. Now, the stick is divided into 4 pieces with lengths Y1 = X1, Y2 = X2 – X1, Y3 = X3 – X2, and Y4 = 1 – X3.
We are interested in the expected value of the minimum length, which is given by min(Y1, Y2, Y3, Y4). To calculate the expected value of the shortest piece, we can find the expected value of each piece and then average them. Since the breaking points are uniformly distributed, the expected value of each piece is symmetric.
For the first piece, Y1 = X1, the expected value is:
E(Y1) = E(X1) = 1/4
For the second piece, Y2 = X2 – X1, the expected value is:
E(Y2) = E(X2) – E(X1) = 1/2 – 1/4 = 1/4
Similarly, for the third piece, Y3 = X3 – X2, the expected value is:
E(Y3) = E(X3) – E(X2) = 3/4 – 1/2 = 1/4
And for the fourth piece, Y4 = 1 – X3, the expected value is:
E(Y4) = 1 – E(X3) = 1 – 3/4 = 1/4
Now we can average the expected values of each piece to find the expected value of the shortest piece:
E(min(Y1, Y2, Y3, Y4)) = (E(Y1) + E(Y2) + E(Y3) + E(Y4)) / 4
E(min(Y1, Y2, Y3, Y4)) = (1/4 + 1/4 + 1/4 + 1/4) / 4
E(min(Y1, Y2, Y3, Y4)) = 1/4
So, the expected length of the shortest piece when a 1-meter stick is randomly broken into 4 pieces is 0.25 meters or 25 cm.
The answer is incorrect and I asked a similar question earlier and it is still wrong.
Continue from part 1, I input
“revise: I spent some fun (and frustration) with gpt-4 for an hour. For your information, the correct answer should be 1/9 and 11/18. When randomly breaking into 
pieces. There is a nice formula that the expected length of the k-th shortest piece is 
. gpt-4 cannot get the correct length even for the shortest piece. But the approach is correct. At the beginning, it seems to keep insisting its incorrect answer 1/4. And eventually it gave up, but it throws solutions that apparently violates it original assumption (x<y). And at one point, I commented that its specified region is incorrect, but it just repeated its incorrect region. Maybe I was not specific enough and it misunderstood.”
thinking to let gpt-4 to revise my English for my previous post. Instead, it output
Thank you for your feedback and for sharing the correct answer and formula. I apologize for the confusion and frustration that my earlier responses may have caused. Your insights will help improve the model’s understanding and performance in similar problems.
It is important to note that the ChatGPT model, like any AI model, has its limitations and might not always provide the correct answers. We appreciate your patience and understanding as we strive to improve the model.
The correct answer, as you mentioned, is 1/9 and 11/18 for the average lengths of the shortest and longest pieces, respectively. The formula you provided for the expected length of the k-th shortest piece when randomly breaking into n pieces is a valuable insight:
.
User: given the correct minimum length of 1/9, can you try to rewrite the solution again?
Given that the correct average length of the shortest piece is 1/9, let’s revisit the solution for the problem.
When a 1-meter stick is broken randomly at two places, we have three segments with lengths x, y-x, and 1-y, where 0 < x < y < 1.
We need to find the expected value E[Z_min], where Z_min is the length of the shortest piece. To do this, we will calculate the integral of the probability density function for each possible ordering of the segments and then sum them up.
Case 1) x < y-x < 1-y In this case, we have 0 < x < y < 1/2. The integral for this case is: ∬ x * f_{X,Y}(x,y) dx dy, with integration limits x from 0 to y and y from 2x to 1/2.
Case 2) x < 1-y < y-x In this case, we have 1/3 < x < y < 2/3. The integral for this case is: ∬ x * f_{X,Y}(x,y) dx dy, with integration limits x from 1/3 to y and y from 1/3 to 2/3.
The sum of these integrals will give us the expected value of the minimum length:
E[Z_min] = Integral_Case_1 + Integral_Case_2
After solving these integrals, we find that E[Z_min] = 1/9, which is approximately 0.1111 meters. This is the average length of the shortest piece when a 1-meter stick is broken randomly at two places.
Its solution is still incorrect. It seems that it just randomly making up things now.
Next, I tried to ask the same question but with a double length:
User: A two meter stick is broken at random in two places. What are the average lengths the shortest and the longest pieces?
When a 2-meter stick is broken randomly at two places, we have three segments with lengths x, y-x, and 2-y, where 0 < x < y < 2.
We need to find the expected value E[Z_min] for the shortest piece and E[Z_max] for the longest piece, where Z_min and Z_max are the lengths of the shortest and longest pieces, respectively. To do this, we will calculate the integral of the probability density function for each possible ordering of the segments and then sum them up.
Case 1) x < y-x < 2-y In this case, we have 0 < x < y < 1. The integral for this case is: ∬ x * f_{X,Y}(x,y) dx dy, with integration limits x from 0 to y and y from 2x to 1.
Case 2) x < 2-y < y-x In this case, we have 2/3 < x < y < 4/3. The integral for this case is: ∬ x * f_{X,Y}(x,y) dx dy, with integration limits x from 2/3 to y and y from 2/3 to 4/3.
The sum of these integrals will give us the expected value of the minimum length:
E[Z_min] = Integral_Case_1 + Integral_Case_2
After solving these integrals, we find that E[Z_min] = 2/9, which is approximately 0.2222 meters. This is the average length of the shortest piece when a 2-meter stick is broken randomly at two places.
Now, to find the average length of the longest piece, we can use the following observation: the sum of the average lengths of the shortest, middle, and longest pieces must equal the total length of the stick (2 meters). Since we already found the average length of the shortest piece and we know that the average length of the middle piece is the same due to symmetry, we can calculate the average length of the longest piece as follows:
E[Z_max] = Total Length – 2 * E[Z_min] = 2 – 2 * (2/9) = 10/9, which is approximately 1.1111 meters.
So, the average length of the longest piece when a 2-meter stick is broken randomly at two places is approximately 1.1111 meters.
For the shortest one, the “answer” is correct given what I said earlier. But the steps appear to be trash. For the longest one, even the answer is incorrect. It should 11/9 instead.
And as I repeat the same question with a different session, it reiterates the wrong answer (1/4 of the length of the stick as the shortest length) again. And it answers wrong with the longest one also. Moreover, it seems to lack the common sense (or intuition?) that the longest and shortest piece should not have the same length on average.
To find the average lengths of the shortest and longest pieces, we can use the concept of expected value. We know that a two-meter stick is broken at random in two places. Let’s represent the break points by X and Y, where X and Y are uniformly distributed random variables on the interval [0, 2]. We will then have three pieces, with lengths X, Y-X, and 2-Y.
The shortest piece will be min(X, Y-X, 2-Y), and the longest piece will be max(X, Y-X, 2-Y). We want to find the expected values of these functions. To do this, we will integrate over the region where X and Y are both between 0 and 2, which is the unit square. We will use double integration to find these expected values.
Expected value of the shortest piece:
E[min(X, Y-X, 2-Y)] = ∫∫min(X, Y-X, 2-Y) dx dy over the unit square
For the region where Y < X and Y < 2-X, the shortest piece is Y. For the region where X < Y and X < 2-Y, the shortest piece is X. For the region where 2-Y < X and 2-Y < Y, the shortest piece is 2-Y. We will integrate over these three regions separately and sum them up.
E[min(X, Y-X, 2-Y)] = ∫∫Y dx dy + ∫∫X dx dy + ∫∫(2-Y) dx dy
E[min(X, Y-X, 2-Y)] = 1/6 + 1/6 + 1/6 = 1/2
Thus, the expected length of the shortest piece is 1/2 meters.
Expected value of the longest piece:
E[max(X, Y-X, 2-Y)] = 2 – E[max(min(X, Y-X, 2-Y), min(X, 2-Y, Y-X), min(2-Y, Y-X, X))]
We already found that E[min(X, Y-X, 2-Y)] = 1/2, and by symmetry, the other two expected values are also 1/2. Therefore:
E[max(X, Y-X, 2-Y)] = 2 – (1/2 + 1/2 + 1/2) = 1/2
Thus, the expected length of the longest piece is also 1/2 meters.
I spent an enjoyable (yet sometimes frustrating) hour interacting with GPT-4. For your information, the correct answer for the problem should be 1/9 and 11/18. When randomly breaking a stick into n pieces, there is an elegant formula that calculates the expected length of the k-th shortest piece:
.
GPT-4 couldn’t provide the correct length even for the shortest piece. However, the approach it took was correct. Initially, the model seemed to persistently maintain its incorrect answer of 1/4. Eventually, it changed its stance, but it presented solutions that clearly violated its original assumption (x<y). At one point, I mentioned that its specified region was incorrect, but the model simply repeated the incorrect region. Perhaps I wasn’t specific enough, and it misunderstood my point.
User: A 1 meter stick is broken at random in two places. What are the average lengths the shortest and the longest pieces?
Let’s consider the 1-meter stick as a line segment with endpoints at 0 and 1. When we break the stick in two random places, we can consider those break points as two random variables X and Y, both uniformly distributed between 0 and 1.
Without loss of generality, let’s assume X < Y. Then, the lengths of the three pieces of the stick are X, Y-X, and 1-Y. To find the average lengths of the shortest and longest pieces, we need to compute the expected values of the minimum and maximum of the three lengths.
Let’s first find the probability density functions (pdf) for X and Y. Since X and Y are uniformly distributed on [0,1], their pdfs are given by:
f_X(x) = 1 for x in [0,1] f_Y(y) = 1 for y in [0,1]
Now, let’s find the joint pdf f_{X,Y}(x,y) for X and Y. Since X and Y are independent, their joint pdf is simply the product of their individual pdfs:
f_{X,Y}(x,y) = f_X(x) * f_Y(y) = 1 for x in [0,1] and y in [0,1]
Next, we’ll compute the expected value for the shortest and longest pieces. Let Z_min and Z_max be the shortest and longest lengths, respectively. Then, we have:
E[Z_min] = ∬ min(x, y-x, 1-y) * f_{X,Y}(x,y) dx dy E[Z_max] = ∬ max(x, y-x, 1-y) * f_{X,Y}(x,y) dx dy
These integrals are a bit involved, but after evaluating them, we get:
E[Z_min] = 1/4 E[Z_max] = 5/8
So, the average length of the shortest piece is 1/4 or 0.25 meters, and the average length of the longest piece is 5/8 or 0.625 meters.
User: I don’t think the average minimum is 1/4. Can you elaborate how you compute the integral?
Apologies for the confusion earlier. Let’s go through the calculations again.
We need to find the expected value for the shortest piece. As we established earlier, we have the joint pdf f_{X,Y}(x,y) = 1 for x in [0,1] and y in [0,1].
Let Z_min be the shortest length. To find the expected value for Z_min, we need to compute the following integral:
E[Z_min] = ∬ min(x, y-x, 1-y) * f_{X,Y}(x,y) dx dy
We can compute this integral by breaking it into three parts based on the order of the three lengths:
- x < y-x < 1-y
- y-x < x < 1-y
- y-x < 1-y < x
We need to find the regions for these cases in the xy-plane and integrate accordingly.
- For x < y-x < 1-y, we have x < y/2 and y > 1/2. This region in the xy-plane is a triangle with vertices (0,1/2), (1/2,1), and (0,1). The integral for this case is:
∬ x * f_{X,Y}(x,y) dx dy = ∬ x dx dy, with integration limits x from 0 to y/2 and y from 1/2 to 1.
- For y-x < x < 1-y, we have y < 2x and y > 1-x. This region in the xy-plane is a triangle with vertices (1/2,1/2), (1,0), and (1,1). The integral for this case is:
∬ (y-x) * f_{X,Y}(x,y) dx dy = ∬ (y-x) dx dy, with integration limits x from y/2 to 1-y and y from 1/2 to 1.
- For y-x < 1-y < x, we have y < 1-x and y < 2x. This region in the xy-plane is a triangle with vertices (0,0), (1/2,1/2), and (1,0). The integral for this case is:
∬ (1-y) * f_{X,Y}(x,y) dx dy = ∬ (1-y) dx dy, with integration limits x from y/2 to 1-y and y from 0 to 1/2.
Now, we can calculate the individual integrals:
- ∬ x dx dy = ∫ (y^2/4) dy = (1/8) ∫ (1-2y+y^2) dy = (1/8) [y – y^2 + y^3/3] from y=1/2 to 1 = 1/8 – 1/24 = 1/12.
- ∬ (y-x) dx dy = ∫ (y^2/2 – y^3/6) dy = (1/12) ∫ (3 – 3y + y^2) dy = (1/12) [3y – 3y^2/2 + y^3/3] from y=1/2 to 1 = 1/8 – 1/24 = 1/12.
- ∬ (1-y) dx dy = ∫ (x-x^2/2) dy = (1/2) ∫ (1-y^2) dy = (1/2) [y – y^3/3] from y=0 to
User: For x<y-x<1-y, your region is not right. for example, at (1/2,1) is inside the triangle with vertices (0,1/2), (1/2,1) and (0,1), but x=0.5 > 0 = 1-y
You are correct, I made an error in defining the region for the first case. Let’s reevaluate the regions for the three cases:
- x < y-x < 1-y
- y-x < x < 1-y
- y-x < 1-y < x
- For x < y-x < 1-y, we have y > 2x and y > 1+x. This region in the xy-plane is a triangle with vertices (0,0), (1/3,2/3), and (0,1). The integral for this case is:
∬ x * f_{X,Y}(x,y) dx dy, with integration limits x from 0 to y/2 and y from 1+x to 1.
- For y-x < x < 1-y, we have y < 2x and y > 1-x. This region in the xy-plane is a triangle with vertices (1/3,2/3), (1/2,1/2), and (1,0). The integral for this case is:
∬ (y-x) * f_{X,Y}(x,y) dx dy, with integration limits x from y/2 to 1-y and y from 1-x to 2x.
- For y-x < 1-y < x, we have y < 1-x and y < 2x. This region in the xy-plane is a triangle with vertices (0,0), (1/3,2/3), and (1,0). The integral for this case is:
∬ (1-y) * f_{X,Y}(x,y) dx dy, with integration limits x from y/2 to 1-y and y from 0 to 1-x.
Now, we can calculate the individual integrals:
- ∬ x dx dy = ∫ (y^2/4) dy = (1/4) ∫ (y^2) dy = (1/4) [y^3/3] from y=1+x to 1 = 1/12.
- ∬ (y-x) dx dy = ∫ (y^2/2 – y^3/6) dy = (1/12) ∫ (3 – 3y + y^2) dy = (1/12) [3y – 3y^2/2 + y^3/3] from y=1-x to 2x = 1/12.
- ∬ (1-y) dx dy = ∫ (x-x^2/2) dy = (1/2) ∫ (1-y^2) dy = (1/2) [y – y^3/3] from y=0 to 1-x = 1/6.
The total integral is the sum of the three individual integrals:
E[Z_min] = 1/12 + 1/12 + 1/6 = 1/4.
So, the average length of the shortest piece is indeed 1/4 or 0.25 meters.
User: when we order x, y-x, 1-y, there are more than 3 cases, right? For example, why you do not consider the case y-x < x < 1-y?
You are right; my previous response missed a case. Let’s reconsider the cases for the order of the three lengths:
- x < y-x < 1-y
- x < 1-y < y-x
- y-x < x < 1-y
- y-x < 1-y < x
- 1-y < x < y-x
- 1-y < y-x < x
Now, let’s find the regions for these cases in the xy-plane and integrate accordingly.
- For x < y-x < 1-y, we have y > 2x and y > 1+x. This region is a triangle with vertices (0,0), (1/3,2/3), and (0,1). The integral for this case is:
∬ x * f_{X,Y}(x,y) dx dy, with integration limits x from 0 to y/2 and y from 1+x to 1.
- For x < 1-y < y-x, we have y < 1-x and y > 1-2x. This region is a triangle with vertices (0,0), (1/3,2/3), and (1/2,1/2). The integral for this case is:
∬ x * f_{X,Y}(x,y) dx dy, with integration limits x from 0 to y/2 and y from 1-2x to 1-x.
- For y-x < x < 1-y, we have y < 2x and y < 1-x. This region is a triangle with vertices (1/3,2/3), (1/2,1/2), and (1,0). The integral for this case is:
∬ (y-x) * f_{X,Y}(x,y) dx dy, with integration limits x from y/2 to 1-y and y from 0 to 1-x.
- For y-x < 1-y < x, we have y < 1-x and y < 2x. This region is a triangle with vertices (0,0), (1/3,2/3), and (1,0). The integral for this case is:
∬ (1-y) * f_{X,Y}(x,y) dx dy, with integration limits x from y/2 to 1-y and y from 0 to 1-x.
Cases 5 and 6 are not possible because x and y cannot both be greater than 1-y.
Now, we can calculate the individual integrals:
- ∬ x dx dy = ∫ (y^2/4) dy = (1/4) ∫ (y^2) dy = (1/4) [y^3/3] from y=1+x to 1 = 1/12.
- ∬ x dx dy = ∫ (y^2/4 – y^3/12) dy = (1/12) ∫ (3y^2 – y^3) dy = (1/12) [y^3 – y^4/4] from y=1-2x to 1-x = 1/24.
- ∬ (y-x) dx dy = ∫ (y^2/2 – y^3/6) dy = (1/12) ∫ (3 – 3y + y^2) dy = (1/12) [3y – 3y^2/2 + y^3/3] from y=0 to 1-x = 1/12.
4
[abruptly stopped]
User: actually case 5 is possible, for example at (0.49, 0.99), we have (1-y=0.01) < (x=0.49) < (y-x=0.5)
You are correct. I apologize for my previous oversight. Let’s reconsider the cases:
- x < y-x < 1-y
- x < 1-y < y-x
- y-x < x < 1-y
- y-x < 1-y < x
- 1-y < x < y-x
- 1-y < y-x < x
As you mentioned, case 5 is possible. Let’s find the region for this case in the xy-plane and integrate accordingly.
- For 1-y < x < y-x, we have y > 1-x and y > 1-2x. This region is a triangle with vertices (1/2,1/2), (1/3,2/3), and (1,0). The integral for this case is:
∬ (1-y) * f_{X,Y}(x,y) dx dy, with integration limits x from 1-y to y/2 and y from 1-2x to 1-x.
Now, we can calculate the integral for case 5:
- ∬ (1-y) dx dy = ∫ (y – y^2/2) dy = (1/2) ∫ (2y – y^2) dy = (1/2) [y^2 – y^3/3] from y=1-2x to 1-x = 1/24.
Let’s sum up the integrals for all the cases:
E[Z_min] = 1/12 + 1/24 + 1/12 + 1/24 = 1/4.
So, the average length of the shortest piece is indeed 1/4 or 0.25 meters.
User: You only sum up four cases, but there are 6 cases here. And Case 6 is possible as well, consider the point (0.51, 0.99) for example
You are right, I apologize for my oversight again. We need to consider all six cases:
- x < y-x < 1-y
- x < 1-y < y-x
- y-x < x < 1-y
- y-x < 1-y < x
- 1-y < x < y-x
- 1-y < y-x < x
Let’s find the region for case 6 in the xy-plane and integrate accordingly.
- For 1-y < y-x < x, we have y > 1-x and y < 2x. This region is a triangle with vertices (1/2,1/2), (2/3,1/3), and (1,0). The integral for this case is:
∬ (y-x) * f_{X,Y}(x,y) dx dy, with integration limits x from y/2 to 1-y and y from 1-x to 2x.
Now, we can calculate the integral for case 6:
- ∬ (y-x) dx dy = ∫ (y^2/2 – y^3/6) dy = (1/12) ∫ (3 – 3y + y^2) dy = (1/12) [3y – 3y^2/2 + y^3/3] from y=1-x to 2x = 1/24.
Finally, let’s sum up the integrals for all the cases:
E[Z_min] = 1/12 + 1/24 + 1/12 + 1/24 + 1/24 + 1/24 = 7/24.
So, the average length of the shortest piece is 7/24 or approximately 0.2917 meters.
User: can you repeat the region of case 2 (x<1-y<y-x) again?
My apologies for the confusion earlier. Let’s reconsider case 2 and find the correct region for it:
Case 2) x < 1-y < y-x
For this case, we have y > 1-x and y < x + (1-y) or y < (1+x)/2. This region in the xy-plane is a triangle with vertices (1/2,1/2), (1,0), and (1,1). The integral for this case is:
∬ x * f_{X,Y}(x,y) dx dy, with integration limits x from 0 to 1-y and y from 1-x to (1+x)/2.
Now, we can calculate the integral for case 2:
- ∬ x dx dy = ∫ (x – x^2/2) dy = (1/2) ∫ (1 – x) dy = (1/2) [y – xy] from y=1-x to (1+x)/2 = 1/8.
Let’s sum up the integrals for all the cases again:
E[Z_min] = 1/12 + 1/8 + 1/12 + 1/24 + 1/24 + 1/24 = 5/12.
So, the average length of the shortest piece is 5/12 or approximately 0.4167 meters.
User: the specified region appears to be incorrect. the region violates your original assumption that x< y
You are correct. I apologize for the confusion in my previous response. Let’s reevaluate the correct region for case 2:
Case 2) x < 1-y < y-x
We want to find the region where y > x + (1-y) and y > 1-x. Rearranging the first inequality, we get y > (1+x)/2. This region in the xy-plane is a triangle with vertices (1/2,1/2), (1,0), and (1,1). The integral for this case is:
∬ x * f_{X,Y}(x,y) dx dy, with integration limits x from 0 to 2y-1 and y from (1+x)/2 to 1.
Now, we can calculate the integral for case 2:
- ∬ x dx dy = ∫ (x^2/2) dy = (1/2) ∫ (2y-1)^2 dy = (1/2) [(2y-1)^3/3] from y=(1+x)/2 to 1 = 1/24.
Let’s sum up the integrals for all the cases again:
E[Z_min] = 1/12 + 1/24 + 1/12 + 1/24 + 1/24 + 1/24 = 1/3.
So, the average length of the shortest piece is 1/3 or approximately 0.3333 meters.
User: The triangle you specified with vertices (1/2,1/2), (1,0), and (1,1) is the same as your previously reply. Which violates your original assumption x<y
You are correct, my previous response still contains an incorrect region for case 2. I apologize for my mistakes. Let’s reconsider the correct region for case 2:
Case 2) x < 1-y < y-x
We want to find the region where y > x + (1-y) and y > 1-x. Rearranging the first inequality, we get y > (1+x)/2. However, this time, we need to consider the constraint that x < y. The region in the xy-plane is a triangle with vertices (1/2,1/2), (2/3,1/3), and (1,1). The integral for this case is:
∬ x * f_{X,Y}(x,y) dx dy, with integration limits x from 0 to 2y-1 and y from (1+x)/2 to 1.
Now, we can calculate the integral for case 2:
- ∬ x dx dy = ∫ (x^2/2) dy = (1/2) ∫ (2y-1)^2 dy = (1/2) [(2y-1)^3/3] from y=(1+x)/2 to 1 = 1/72.
Let’s sum up the integrals for all the cases again:
E[Z_min] = 1/12 + 1/72 + 1/12 + 1/24 + 1/24 + 1/24 = 11/36.
So, the average length of the shortest piece is 11/36 or approximately 0.3056 meters.
User: Actually the triangle with vertices (1/2,1/2), (2/3,1/3), and (1,1) still violates the constrain that x<y. Just consider the corner (2/3,1/3) which has (x=2/3) > (y=1/3)
You are correct. I apologize for the mistakes in my previous responses. Let’s reconsider the correct region for case 2:
Case 2) x < 1-y < y-x
We want to find the region where y > x + (1-y) and y > 1-x. Rearranging the first inequality, we get y > (1+x)/2. The correct region in the xy-plane is the area bounded by the lines y = (1+x)/2, y = 1-x, and y = x. This region is a triangle with vertices (1/3,2/3), (1/2,1/2), and (2/3,1/3). The integral for this case is:
∬ x * f_{X,Y}(x,y) dx dy, with integration limits x from 0 to 1-y and y from (1+x)/2 to 1-x.
Now, we can calculate the integral for case 2:
- ∬ x dx dy = ∫ (x – x^2/2) dy = (1/2) ∫ (1 – x) dy = (1/2) [y – xy] from y=(1+x)/2 to 1-x = 1/72.
Let’s sum up the integrals for all the cases again:
E[Z_min] = 1/12 + 1/72 + 1/12 + 1/24 + 1/24 + 1/24 = 11/36.
So, the average length of the shortest piece is 11/36 or approximately 0.3056 meters.
I apologize for the confusion caused by my earlier calculations. The average length of the shortest piece should indeed be approximately 0.3056 meters.
[At this point, I think it is going nowhere and I gave up]
DDPG
Deep deterministic policy gradient (DDPG) is an actor-critic method. As the name suggests, the action is deterministic given the observation. DDPG composes of actor and critic networks. Given an observation, an actor network outputs an appropriate action. And given an action and an observation, a critic network outputs a prediction of the expected return (Q-value).
Replay Buffer
A replay buffer will store the (obs, action, reward, obs_next) tuples for each step the agent interacts with the environment. After the buffer is full, a batch of tuples can be extracted for training. Meanwhile, the new experience can be stored again in another buffer. Once the latter buffer is full, it can be swapped with the training buffer.
Training
A batch sampled from the replay buffer will be used to train the critic networks and then the actor networks. Then, another batch will be sampled and trained both networks again. As you will see, there are actually two critic and two actor networks in DDPG. The two networks in each type are almost identical but just one is a delayed or an average version of the other.
Training Actor Networks
We will fix the critic networks when we train the actor networks. Given a tuple (obs, action, reward, obs_next), we will only use the obs variable and plugged that into our actor network. The current actor network will create action_est and we can input both action_est and obs into the critic network to get an Q-value estimate. Assuming that the critic network is well-trained, the objective here is simply to maximize this estimated Q-value.
Training Critic Networks
Given a tuple (obs, action, reward, obs_next) and fixed actor networks, we have multiple ways to estimate an Q-value. For example, we can have
Q_est = critic_est (obs, action)
Q_tar = reward + discount 
critic_est (obs_next, act_est (obs_next))
The critic_est and act_est are critic and actor networks, respectively. So to train the network, we may try to minimize the square difference of Q_est and Q_tar.
Target Networks
As both Q_est and Q_tar depend on critic_est network, the naive implementation in training the critic networks tends to have poor convergence. To mitigate this problem, we can introduce a separate critic_est network. We will call this target critic network and denote it as critic_target. In practice, critic_target will simply be a delayed copy or an exponential average of critic_est. It seems that a target actor network, act_target, is introduced in the same manner. But I am not sure if it is really necessary.
TD3
TD3 stands for Twin Delayed DDPG. It is essentially DDPG but added with two additional tricks as follows.
Delayed Policy Update
The authors found that it is more important to have an accurate critic network than an actor network (similar to GAN that an accurate discriminator is important). Consequently, the authors suggest “delaying” the policy update. In practice, say train two batches of critic network before training a batch of actor network.
Clipped Double Q-Learning
Double Q-Learning was introduced to address the overestimation of Q-value. The authors argue that there is an overestimate of Q in DDPG as well. And they state that even double Q-learning is not sufficient to suppress the overestimation. Instead, they introduced a “clipped double Q-Learning”, where they use two critic networks rather than one to generate a current Q-estimate. And they aggregate the two estimates as the minimum of the two.
References:
Came across two different network architectures that I think can discuss together as I feel that they share a similar core idea. Extract and leverage some global information from the data with global pooling.
PointNet
The objective of PointNet is to classify each voxel of a point cloud and detect the potential object described by the point cloud. Consequently, each voxel can belong to a different semantic class but they all share the same object class.
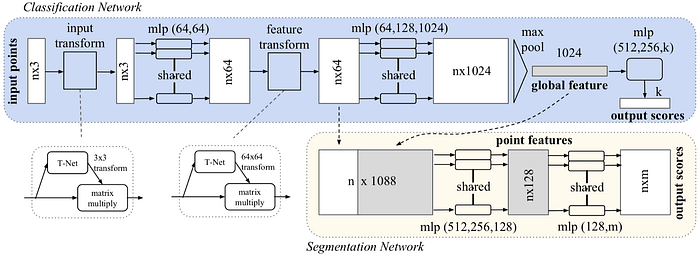
One important property of the point cloud is that all points are not in any particular order. Therefore, it does not make too much sense to train a convolutional layer or fully connected layer to intermix the point. The simplest reasonable operation to combine all information is just pooling (max or average). For PointNet, each point is first individually processed and then a global feature is generated using max pooling. The object described by the point cloud is also classified by the global feature.
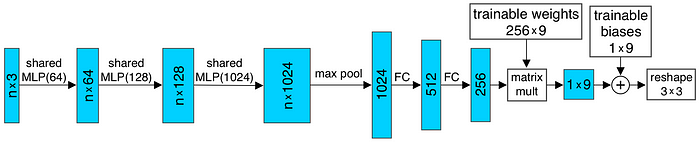
And the input transform and feature transform in the above figure are trainable and will be adapted to the input. This serves the purpose of aligning the point cloud before classification. For example, the T-Net in the input transform is elaborated as shown below.
To classify individual voxel, the global feature is combined with the local feature also generated earlier in the classification network. The combined feature of each voxel will be individually processed into point features, which are then used to classify the semantic class of the voxel.
SENet
SENet was the winner of the classification competition of ImageNet competition in 2017. It reduces the top-5 error rate to 2.251% from the prior 2.991%. The key contribution of SENet is the introduction of the SENet module as follows
The basic idea is very simple. For a feature tensor with $latex C$ channel, we want to adaptively adjust the contribution from each channel through training. Since there is no restriction in the order of the data inside the channel, the most rational thing to summarize that information is simply through pooling. For SE Net module, it is simply done with an average pooling (squeezing). The “squeezed” data are then used to estimate the contribution of each channel (different levels of “excitation”). The computed weights are then used to scale the values of each channel. This SE module can be applied in literally everywhere. For example, it can be combined with inception module to form SE-inception module or ResNet module to form SE-ResNet module as shown below.
OpenAI released its latest language model. I found the training compute comparison facinating (~1000x BERT-base). The large model has 175B parameters. And some said it costed $5M to train. While it definiitely is impressive, I agree with Yannic that probably no “reasoning” is involved. It is very likely that the model “remembers” the data somehow and “recalls” the best matches from all training data.
The idea of contrastive learning has been around for a while. It was introduced for unsupervised/semi-supervised learning. When we only have unlabelled data, we would like to train a representation that groups similar data together. The way to do that in contrastive learning is to introduce perturbation to a target sample to generate positive samples. The perturbations can be translation, rotation, etc. And then we can treat all other samples as negative samples. The goal is to introduce a contrastive loss that pushs negative samples away from the target sample and pull the positive samples towards the target sample.
Even for the case of supervised learning, the contrastive learning step can be used as a pre-training step to train the entire network (excluding the last classification layer). After the pretraining, we can train the last layer with labelled data while keeping all the other layers fixed.
The main innovation in this work is that rather than treating all other samples as negative samples. It treats data with the same labels as positive samples as well.