Here I will derive Kalman filter from belief propagation (BP). While I won’t derive exactly the closed-form expression as Kalman filter, one can verify numerically that the BP procedure below is the same as the standard Kalman filter. For derivation to the exact same expression, please see here.
Kalman filter is a special case of Gaussian BP. It can be easily understood as three different propagation steps as below.
Scenario 1: Passing message from 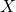 to
to 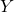 for
for 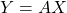
Say ![]() ,
, ![]() . And as
. And as
![]()
![]() .
.
Therefore, ![]() .
.
Scenario 2: Passing message from 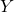 back to
back to 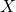 for
for 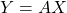
This is a bit trickier but still quite simple. Let the covariance of ![]() be
be ![]() . And from the perspective of
. And from the perspective of ![]() ,
,
![]()
![]()
![]()
![]()
![]()
Thus, ![]()
Scenario 3: Combining two independent Gaussian messages
Say one message votes for ![]() and precision
and precision ![]() (precision is the inverse of the covariance matrix). And say another message votes for
(precision is the inverse of the covariance matrix). And say another message votes for ![]() and precision
and precision ![]() .
.
Since
![]()
![]()
![]()
![]()
Thus, ![]()
BP for Kalman update
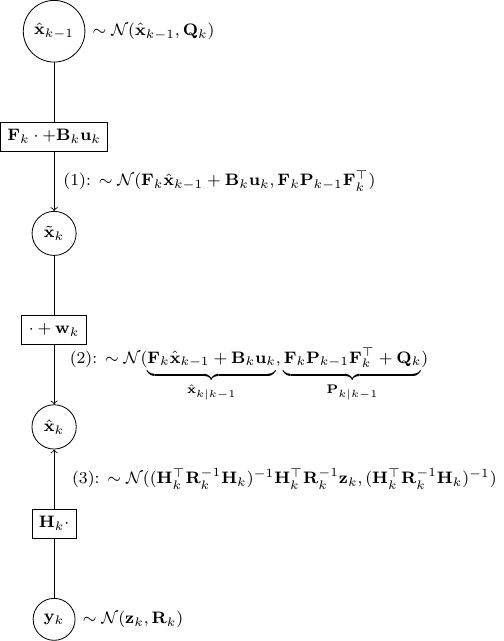
Let’s utilize the above to derive the Kalman update rules. We will use almost exactly the same notation as the wiki here. We only replace ![]() by
by ![]() and
and ![]() by
by ![]() to reduce cluttering slightly.
to reduce cluttering slightly.
- As shown in the figure above, given
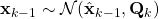 and
and 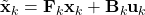 , we have as in (1)
, we have as in (1)
![Rendered by QuickLaTeX.com \[\tilde{\bf x}_k \sim \mathcal{N}({\bf F}_k \hat{\bf x}_{k-1} + {\bf B}_k {\bf u}_k, {\bf F}_k {\bf P}_{k-1}{\bf F}_k^\top)\]](https://outliip.org/wp-content/ql-cache/quicklatex.com-53c4647000975eab4573bbd27baa466c_l3.png)
as it is almost identical to Scenario 1 besides a trivial constant shift of
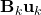 .
. - Then step (2) is obvious as,
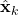 is nothing but
is nothing but 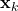 added by a noise of covariance
added by a noise of covariance 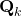 .
. - Now, step (3) is just a direct application of Scenario 2.
Finally, we should combine the estimate from (2) and (3) as independent information using the result in Scenario 3. This gives us the final a posterior estimate of ![]() as
as
![Rendered by QuickLaTeX.com \[\mathcal{N}\left(\Sigma({\bf P}_{k|k-1}^{-1} \hat{\bf x}_{k|k-1} +{\bf H}_k^\top {\bf R}_k^{-1} {\bf z}_k),\underset{\Sigma}{\underbrace{({\bf P}^{-1}_{k|k-1}+{\bf H}^\top_k {\bf R}^{-1}_k {\bf H}_k)^{-1}}}\right)\]](https://outliip.org/wp-content/ql-cache/quicklatex.com-f728e11ea7c6193a812c8c9305dcdd48_l3.png)
Although it is not easy to show immediately, one can verify numerically that the ![]() and the mean above are indeed
and the mean above are indeed ![]() and
and ![]() in the original formulation, respectively.
in the original formulation, respectively.