Latest 3D inpainting result is amazing. See paper and video.
Month: July 2020
Watched the first lecture of underactuated robotics by Prof Tedrake. It was great. His lecture note/book is available online. And the example code is directly available at colab.
So what is underactuated robotics? Consider a standard manipulator equation with state $latex q$
$latex M(q) \dot{q}+C(q,\dot{q}) \dot{q} = \tau_g(q) + B(q) u,$
where L.H.S. are the force terms, R.H.S. are the “Ma” terms, $M(q)$ is mass/inertia matrix and positive definite, $latex u$ is the control input, and $latex B(q)$ maps the control input to $latex q$.
We can rearrange the above to
$latex \ddot{q}= M(q)^{-1} [ \tau_g(q) + B(q) u – C(q,\dot{q} )\dot{q}] =\underset{f_1(q,\dot{q})}{\underbrace{M(q)^{-1}[ \tau_g(q) – C(q,\dot{q} )\dot{q}]}} +\underset{f_2(q,\dot{q})}{\underbrace{M(q)^{-1} B(q) }}u .$
Note that if $latex f_2(q,\dot{q})$ has full row rank (or simply $latex B(q)$ has full row rank since $latex M(q)$ is positive definite and hence full-rank), then for any desired $latex \ddot{q}^d$, we can achieve that by picking $latex u$ as
$latex u = f_2^{\dagger} (q,\dot{q}) (\ddot{q}^{d} – f_1(q,\dot{q})),$ where $latex f_2^{\dagger}$ is the pseudo-inverse of $latex f_2$. We say such robotic system is fully actuated.
On the other hand, if $latex f_2(q,\dot{q})$ does not have full row rank, the above trivial controller will not work. We then have a much more challenging and interesting scenario. And we say the robotic system is underactuated.
A very nice visualization to explore NLP papers
It is kind of mysterious that this works without using negative samples for self learning. See video and paper
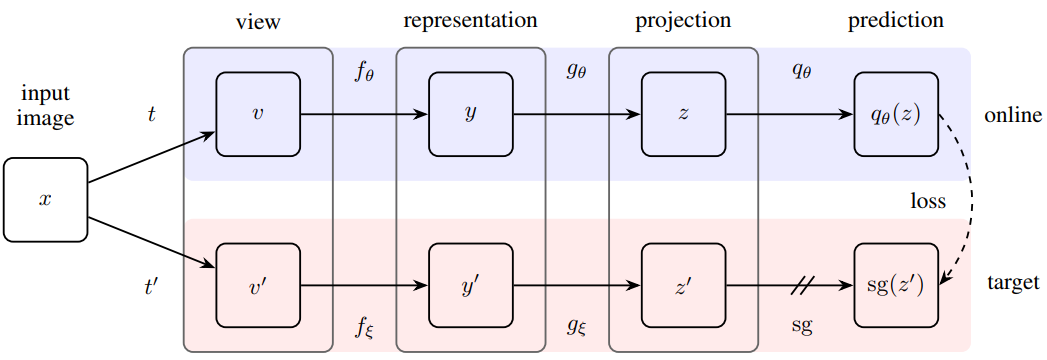
- The main idea is to train a representation network and a classifier so that the latter will predict the representation of an augmented data input.
- The representation network for the augmented data has moving average parameter of the current representation. Similar tricks have been used in deep reinforcement learning
- It is indeed quite surprising that this works without negative samples. Because there is nothing in the above model that avoids converging to trivial solution (everything maps to a constant)
- Experimental results look good. But also may not be accounted for too much. Their implementation for some older approaches have way higher prediction performance. And they pulled numbers from papers (reasonable tho) for comparison. Approach is probably on par and without negative samples, they can train with a smaller batch size
- They are using 512 TPUs for training for 7 hours…
Remarks:
- Project embedding to lower dimension to save computational complexity and space
- Some gain in speed but doesn’t look too significant. Tradeoff in performance seems larger than claimed
- Theorem 1 based on JL-lemma did not used properties of attention itself. It seems that the same argument can be used to anywhere (besides attention). The theorem itself seems to be a bit a stretch
- With the same goal of speeding up transformer, the “kernelized transformer” appears to be a better work
tldr. but the routing mechanism here seems to be quite similar with the capsule one. The authors emphasize that a slot should learn not just one type of object. It seems that the main trick is to first route image feature to slots. Slots will then be train to fit not just one type of objects like capsule network.